X 2 4x 6 = 0 Step 2 Parabola, Finding the Vertex 21 Find the Vertex of y = x 24x6 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum)The vertex form of a quadratic is given by y = a(x – h) 2 k, where (h, k) is the vertex The "a" in the vertex form is the same "a" as in y = ax 2 bx c (that is, both a's have exactly the same value) The sign on "a" tells you whether the quadratic opens up or opens downWrite the equation y = x^2 4x 12 in vertex form Sketch the graph of the equation y = x^2 4x 12 Sketch the graph of the equation 4y = 4 x^2 Determine the focus and directrix of this parabola Match the equations to the graphs i y = x^3 ii y = 3 3x^2 x^3 iii y = 3x(x^2 1)
How Do You Find The Vertex Of Y 2x 2 4x Socratic
Y=x^2-4x+6 in vertex form
Y=x^2-4x+6 in vertex form- y = (x2)^2 2 >the standard form of a quadratic function is y = ax^2 bx c here f(x) = x^2 4x 6 and by comparison a = 1 , b = 4 and c = 6 in vertex form the equation is y = a(xh)^2 k where ( h , k ) are the coords of the vertex the xcoord of vertex = b/(2a) = 4/2 = 2 and ycoord =(2)^2 4(2) 6 = 4 8 6 = 2 now (h , k) =(2 , 2) and a = 1 rArr y = (x2)^2 2Here, the vertex is (h, k) Solved Examples Example 1 Write the following quadratic function in vertex form and sketch the parabola y = x 2 4x 3 Solution Step 1 In the quadratic function given, the coefficient of x 2 is 1 So, we can skip step 1 Step 2 In the quadratic function y = x 2 4x 3, write the "x" term as a multiple




Swbat Using Completing The Square To Put A
This shows us that the solutions to the equation \(ax^2bxc=0\) are \(\frac{b\pm\sqrt{b^24ac}}{2a}\text{}\) Subsection 1333 Putting Quadratic Functions in Vertex Form In Section 132, we learned about the vertex form of a parabola, which allows us to quickly read the coordinates of the vertexWe can now use the method of completing the square to put a quadratic function in vertex formAlso, the general form of equation of parabola with a vertex (h,k) can be written as {eq}\displaystyle { y = a(xh)^2k, } {/eq} where a is a parameter which determines the Put the quadratics below into vertex form by completing the square state the vertex a) y=x^2 – 4x21 asked by Lily on Math Put the quadratics below into vertex form by completing the square state the vertex y=2x^2 – 4x6 asked by Lily on Math
Convert to vertex form by completing the square 1 y = x 2 4x 2 y = x 2 2x 5 3 y = x 2 14x 59 4 y = 2x 2 36x 170So today we're going to change this final meal X squared minus six X plus two into vortex form First thing you do is you take the two terms X squared, minus six X You're gonna leave this blank for61 Write Parabola in standard form and identify its vertex y=x^24x2 61 Write Parabola in standard form and identify its vertex y=x^24x
Find the Vertex Form y=x^24x6 Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Cancel the common factor of and Tap for more steps Factor out ofMove the constant over to achieve vertex form is the final answer with vertex at (1,7) Note that the formula is try this shortcut after you have mastered the steps Make sure you recognize that this formula gives you an x and y coordinate for the vertex and that each coordinate of the pair is fraction in the formulaIn the Desmos graph, activate "Show vertex" by clicking on the circle to the left of the statement For each row in Table 261, slide the values of \(h\) and \(k\) in the Desmos graph to the values stated in the tablerow and make note of the vertexLook for a pattern In the Desmos graph, change the value of \(a\) to anything you like (other than \(0\)) and repeat the exercise




Vertex Form Equation Functions Video Lesson Transcript Study Com



Practice 1 2 Graphing In Vertex Form And Intercept Form
We can convert to vertex form by completing the square on the right hand side;STEP 6 Finally, express the trinomial inside the parenthesis as the square of binomial and then simplify the outside constants Be careful combining the fractions It is now in the vertex form y = a{\left( {x h} \right)^2} k where the vertex \left( {h,k} \right) is \large\left( {{{ \,3} \over 2},{{ 11} \over 2}} \right)By comparing this with the vertex form of parabola, we get (h, k) ==> (1, 9) Example 6 y = (x1)(x3) Solution y = x 24x3 y = x 22 ⋅ x ⋅2 2 22 2 3 y = (x2) 243 y = (x2) 21 By comparing this with the vertex form of parabola, we get (h, k) ==> (2, 1) Example 7 y = 3(x1) 2 Solution y = 3(x1) 2 0




Example 4 Write A Quadratic Function In Vertex Form Write In Vertex Form Then Identify The Vertex X 2x 2 10x 22 Y Solution X 2x 2 10x 22 Y Write Ppt Download




How To Find The Vertex Of A Quadratic Equation 10 Steps
The vertex of a quadratic equation in vertex form is (h,k), so our vertex is (360 seconds Q Which of the following equations shows the vertex form of a quadratic?11, 12 Graphing and Vertex Form, Standard Form, Intercept/Factored Form, 15 Square Roots



Vertex Form Of A Quadratic Function Worksheet




Converting Quadratic Equations Worksheet Coach Forrester
Vertex form y= (x2)^2–12 or y16=(x2)^2 Here's my work 1 The given standard form equation y=x^2–4x12 2 Adding 12 on both sides 3 1 y12=x^2–4x 4 Completing the perfect square on the right side of the equation by adding 4 to both sides of Makeup a quadratic equation in standard form with the following properties a not equal to 1 or 0, b not equal to 0 and c not equal to 0 Complete the square to change the relation to vertex form * math A parabola passes through the point (3, 5) on its way to the vertex at (7, 11) Determine the equation in vertex form that represents this parabola If a quadratic function is given in vertex form, it is a simple matter to sketch the parabola represented by the equation For example, consider the quadratic function \f(x)=(x2)^{2}3\ which is in vertex form The graph of this equation is a parabola that opens upward It is translated 2 units to the left and 3 units upward




How To Solve The Vertex Form Of A Quadratic Equation Sola Education




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21
Create your account View this answer Given y =x24x−1 y = x 2 4 x − 1 The vertex form of a parabola is given by (y−k) = (x−h)2 ( y − k) = ( x − h) 2 The given expression isSal rewrites the equation y=5x^2x15 in vertex form (by completing the square) in order to identify the vertex of the corresponding parabolaAdding 18 to both sides gives us a perfect square trinomial on the right;



Www Cravenk12 Org Cms Lib Nc Centricity Domain 1711 Unit 2 test quadratics review Pdf




The Vertex Form Of The Function Is Choose The Equation That Shows A Step In The Process Of Brainly Com
I write the function of y = x^2 14x 11 into vertex form About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features ©Solved by pluggable solver Completing the Square to Get a Quadratic into Vertex Form Start with the given equation Add to both sides Factor out the leading coefficient Take half of the x coefficient to get (ie )F (x) = x 2 4x 12 Q What is the yintercept of Q Write y = x 2 4x 1 in vertex form



1 Y X 1 1 Convert The Following Quadratics Chegg Com




Graph The Parabola Y X 2 4x 1 Youtube
Step 1 use the (known) coordinates of the vertex, ( h, k), to write the parabola 's equation in the form y = a ( x − h) 2 k the problem now only consists of having to find the value of the coefficient a Step 2 find the value of the coefficient a by substituting the coordinates of point P into the equation written in step 1 and solvingOne formula works when the parabola's equation is in vertex form and the other works when the parabola's equation is in standard form Standard Form If your equation is in the standard form $$ y = ax^2 bx c $$ , then the formula for the axis of symmetry is $ \red{ \boxed{ xWe want to put it into vertex form y=a(xh) 2 k;
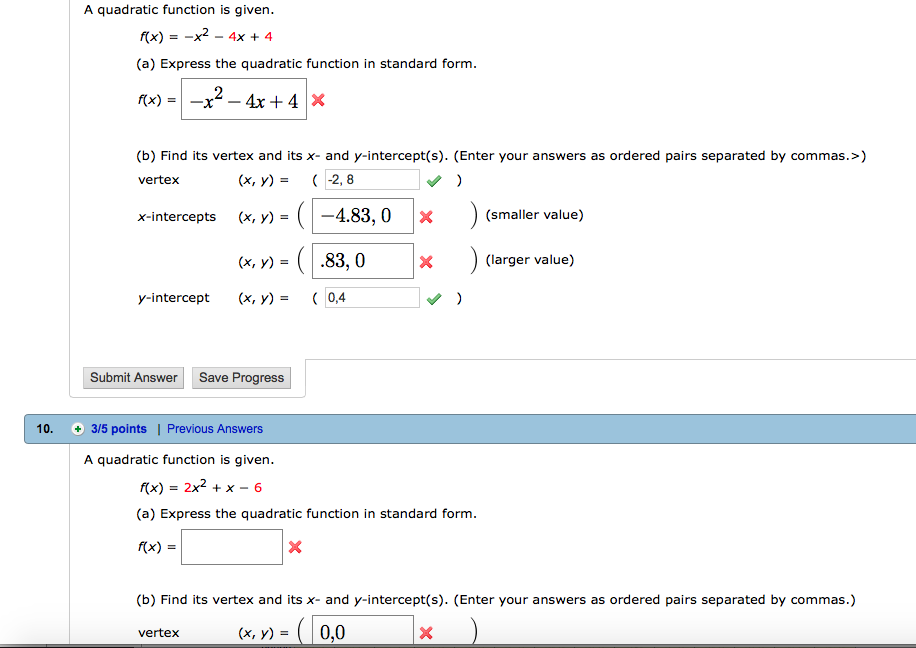



A Quadratic Function Is Given F X X 2 4x 4 Chegg Com



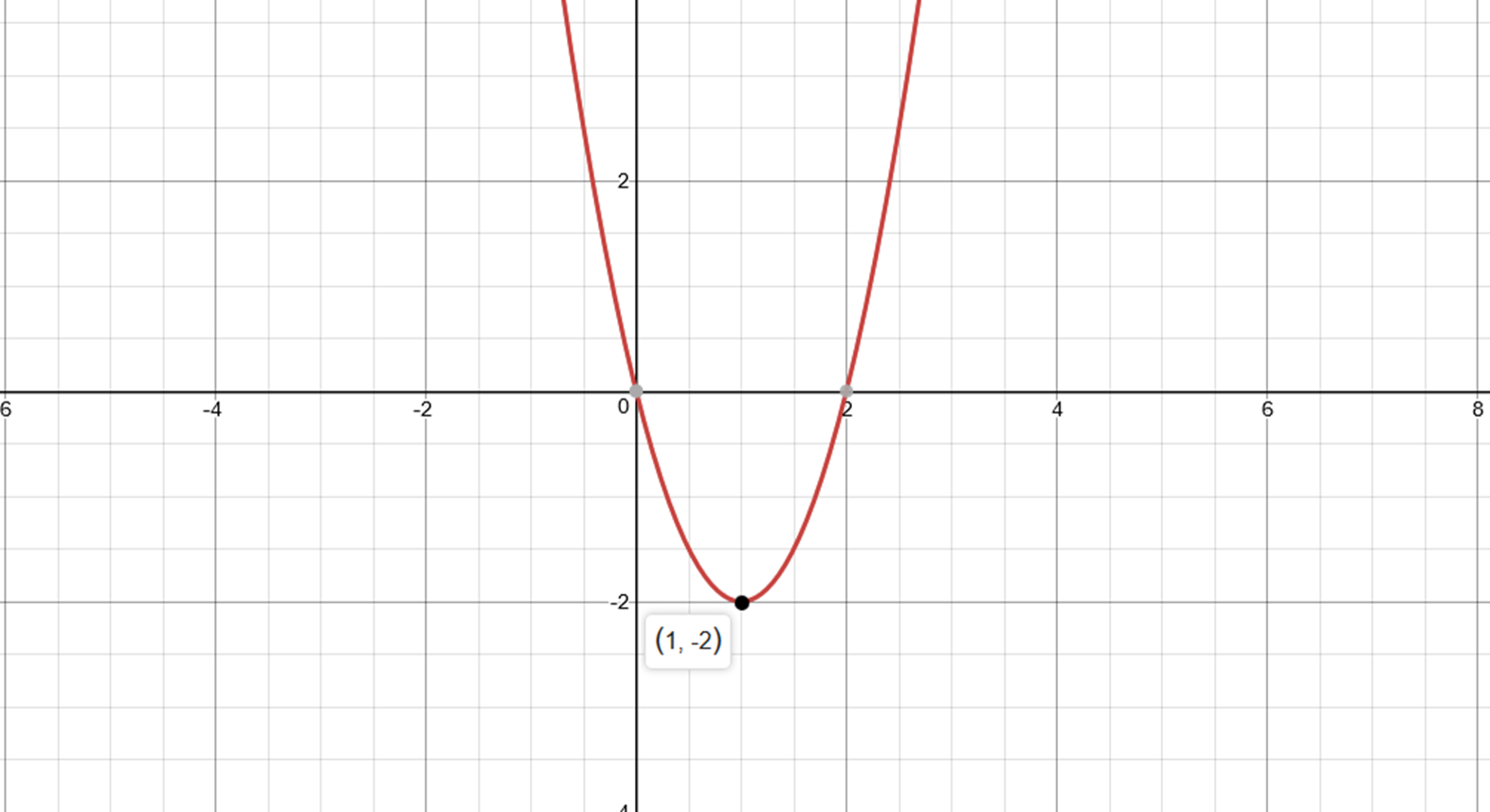
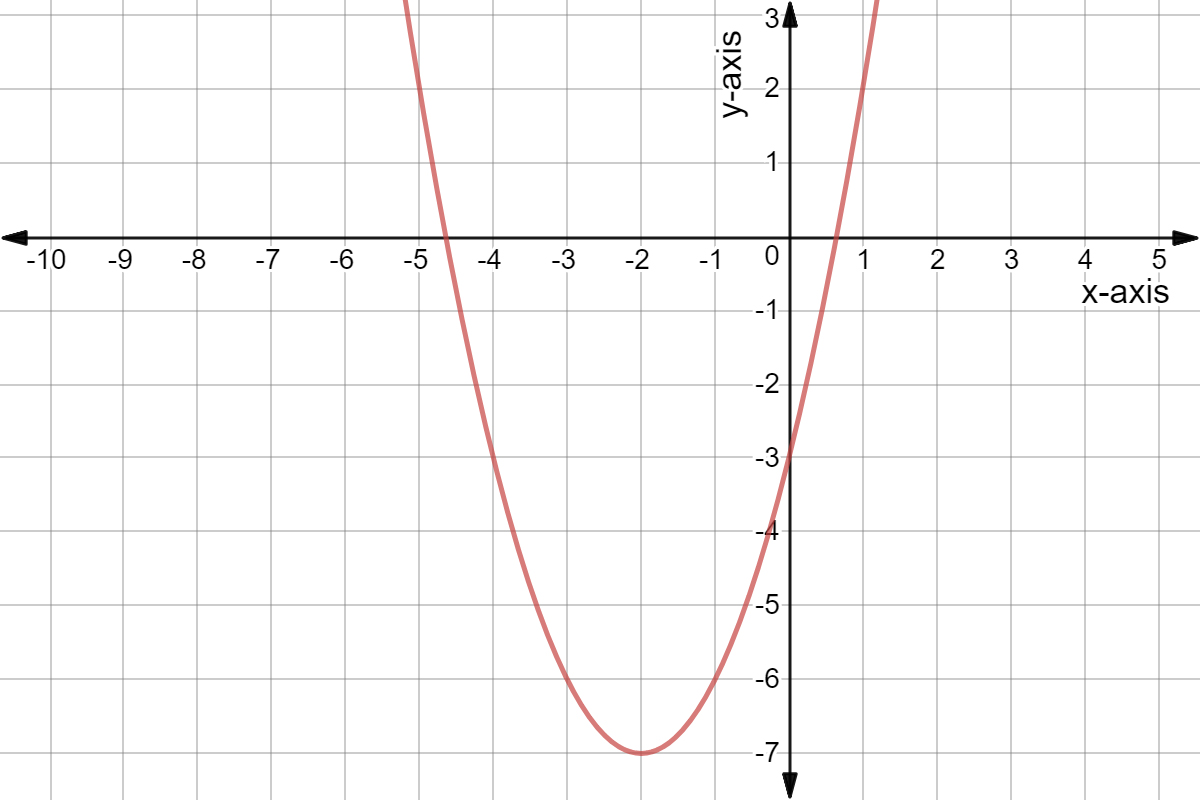
Y X2 4x 6 Math Homework Answers
Write y= x^2 4x 6 in vertex form NEED ASAP!! 👍 Correct answer to the question Given the equation y = x^24x9, write in vertex form where y = a(x−h)2k eeduanswerscomThe vertex form of equation is \displaystyle{y}={4}{\left({x}\frac{{1}}{{2}}\right)}^{{2}}{2} Explanation \displaystyle{y}={4}{x}^{{2}}{4}{x}{1} or \displaystyle{y}={4}{\left({x}^{{2}}{x}\right)}{1}




Find Factored Form And Vertex Of F X 2x 2 4x 6 Youtube



How Do You Find The Vertex Of F X 2x 2 4x 6 Socratic
When we have the equation of a parabola, in the form y = ax^2 bx c, we can always find the x coordinate of the vertex by using the formula x = b/2a So we just plug in the values In this case, the equation in form y = ax^2 bx c is equal to y=x^2 4x 122 Quadratics in Vertex Formnotebook 1 Apr AM DO NOW Find the axis of symmetry and the vertex of y = 2x 2 6x 7 algebraically Apr 159 AMX 2 4x 6 = 0 Step 2 Parabola, Finding the Vertex 21 Find the Vertex of y = x 24x6 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum)




Please Help Asap Write The Equation Of The Parabola In Vertex Form A Y X 2 2 4b Y Brainly Com
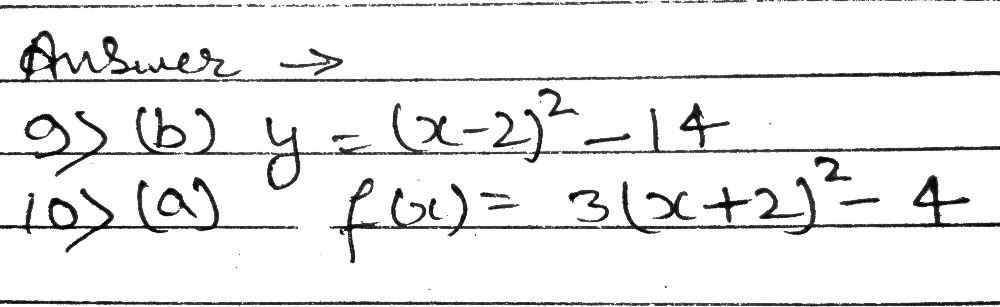



9 Transform Y X2 4x 10 Into The Form Y Ax H2 K A Gauthmath
rewrite function in vertex form y=x^24x12 rewrite function in vertex form y=x^24x12 Answer To see more answers head over to College Study Guides Virtual Teaching Assistant John B Question Level Basic Karma Free Upload Date This 12 words question was answered by John B on StudySoup on The question containsVertex\y=x^ {2}2x3 vertex\y=3x^ {2}5x vertex\y=x^ {2} vertex\y=2x^ {2}2x2 functionvertexcalculator enTo find the vertex just use the equation x= (b)/ (2*a) so the first one would be 1 y=x^24x6 x= (4)/ (2*1) x= 2 the rest i am just going to put in the answers 2 1 3 0 4 0




Solved Example 1 Y X2 4x 6 Graphing Quadratic Func Chegg Com




Y Classzone
Review Vertex and Intercepts of a Quadratic Functions The graph of a quadratic function of the form f(x) = a x 2 b x c is a vertical parabola with axis of symmetry parallel to the y axis and has a vertex V with coordinates (h , k), x intercepts when they exist and a y intercept as shown below in the graph When the coefficient a is positive the vertex is the lowest point in theOur equation is in standard form to begin with y=ax 2 bxc;The vertex form of the function given is texy = (x 2)^2 3/texThe vertex form of a quadtratic function is in the form texy = (x h)^2 k/texStart by
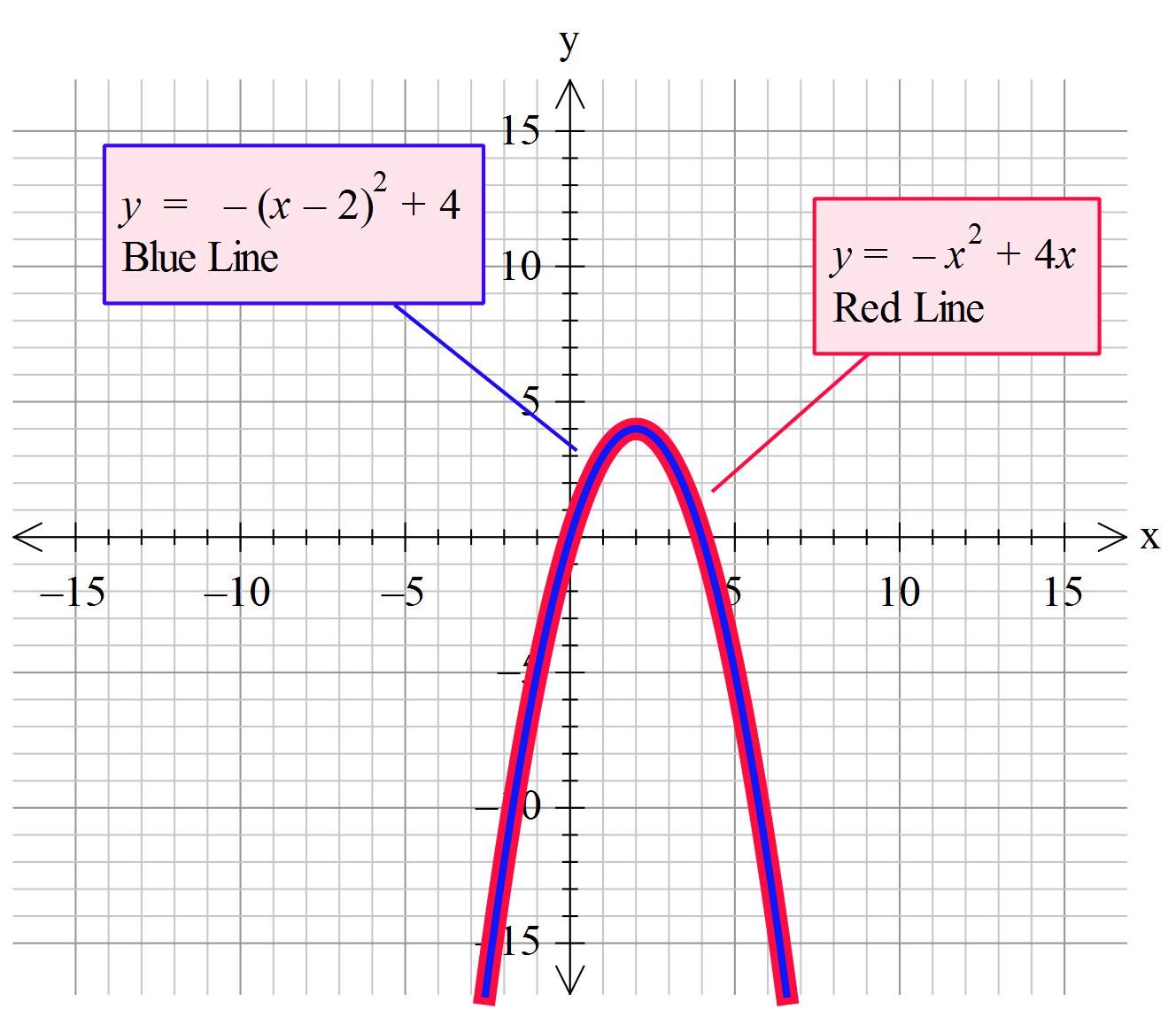



How Do You Write F X X 2 4x In Vertex Form Socratic




Vertex To Standard Form Calculator Mike S Calculators With Steps Free 21
Find the Vertex y=x^24x6 Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Cancel the common factor of This is one way of doing it We want to get the function into vertex form y = x 2 4x 2 Subtract 2 from both sides y 2 = x 2 4x Add (4/2) 2 , or 4, to both sides y 2 4 = x 2 4x 4 Now that the right hand side is a perfect square trinomial, factor it y 2 = (x 2) (x 2)3 3 2 Explanation graph{(y(x^24x5))(y(2x8))=0 5, 5, 5, 12} First we solve the simultaneous equations {y = x 2 − 4 x 5 y = − 2 x 8 Two parabolas are the graphs of the equations y=2x^210x10 and y=x^24x6 give all points where they intersect list the points in order of increasing xcoordinate, separated by semicolons




Converting Quadratics Vertex Form To Standard 13 Write An Equation For A Parabola With Vertex Pdf Document



Www Sanjuan Edu Site Handlers Filedownload Ashx Moduleinstanceid 598 Dataid Filename Unit 3 final review answers Pdf
The vertex form is a special form of a quadratic function From the vertex form, it is easily visible where the maximum or minimum point (the vertex) of the parabola is The number in brackets gives (trouble spot up to the sign!) the xcoordinate of the vertex, the number at the end of the form gives the ycoordinate This means If the vertex form is , then the vertex is at (hk) How to put a function into vertex form?The graph of a quadratic function is called a Q The quadratic parent function Q What is the axis of symmetry of the given function?Get the answers you need, now!




Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube




Solved Consider Y X 2 X 6 This Equation Is Give Chegg Com
More y = a (xh)^2 k is the vertex form equation Now expand the square and simplify You should get y = a (x^2 2hx h^2) k Multiply by the coefficient of a and get y = ax^2 2ahx ah^2 k This is standard form of a quadratic equation, with the normal a, b and c in ax^2 bx c equaling a, 2ah and ah^2 k, respectivelyY = x^2 4x 6 Answer by jim_thompson5910 () ( Show Source ) You can put this solution on YOUR website!Converting From Standard Form to Vertex Form It is more difficult to convert from standard form to vertex form The process is called "completing the square" Conversion When latexa=1/latex Consider the following example suppose you want to write latexy=x^24x6/latex in vertex form



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora




Parabolas Part 2 I Vertex Form Of A
Answer choices x = b/2a x = (b ±√b 2 4ac)/2a y = ax 2 bx c y = a (x h) 2 k How to solve for vertex form y = x^2 4x – 1 Answers 2 Get Other questions on the subject Mathematics Mathematics, 1330, mbatton879 In the coordinate plan (6,9) b (3,9) c (3,3) def is shown in the coordinate plan below Answers 1 continueGraphing a Quadratic Equation Using a Table of Values b Graph y x 2 4x 6 in the interval 1 x 5 x 2a ( 4) x y x 1 1 Axis of 2(1) Symmetry 0 6 4 1 9 x=2 x 2 2 10 x 2 3 9 4 6 5 1 That was easy Vertex (2, 10) Graphing Examples x y Quadratic Functions Function f ( x ) ax bx c 2 Standard Form (Vertex Form) f ( x) a( x h)2 k Graphs a
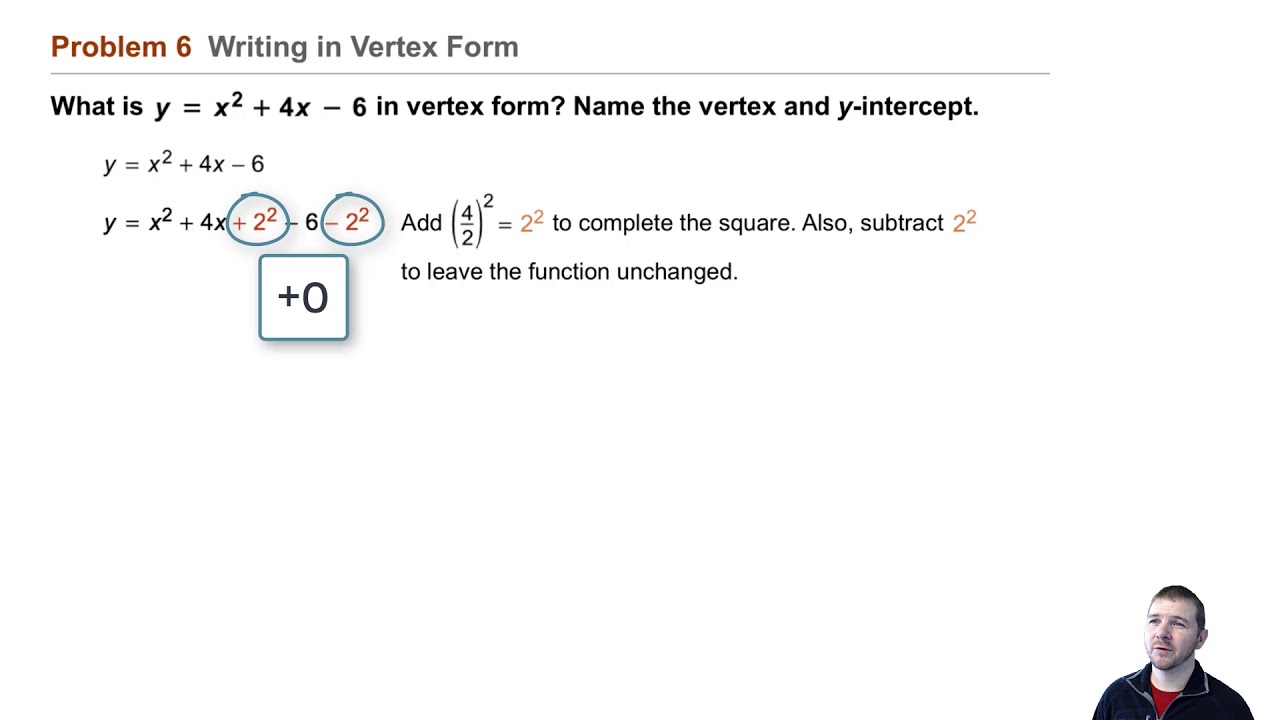



Algebra 2 4 6 Completing The Square Problem 6 Writing In Vertex Form Youtube




Example 6 Write A Quadratic Function In Vertex



Completing The Square Vertex Form Of A Quadratic Expii



1




4 7 Write In Vertex Form




5 Write The Equation Of The Parabola In Vertex Form Chegg Com



Graphing Quadratic Functions




Swbat Using Completing The Square To Put A
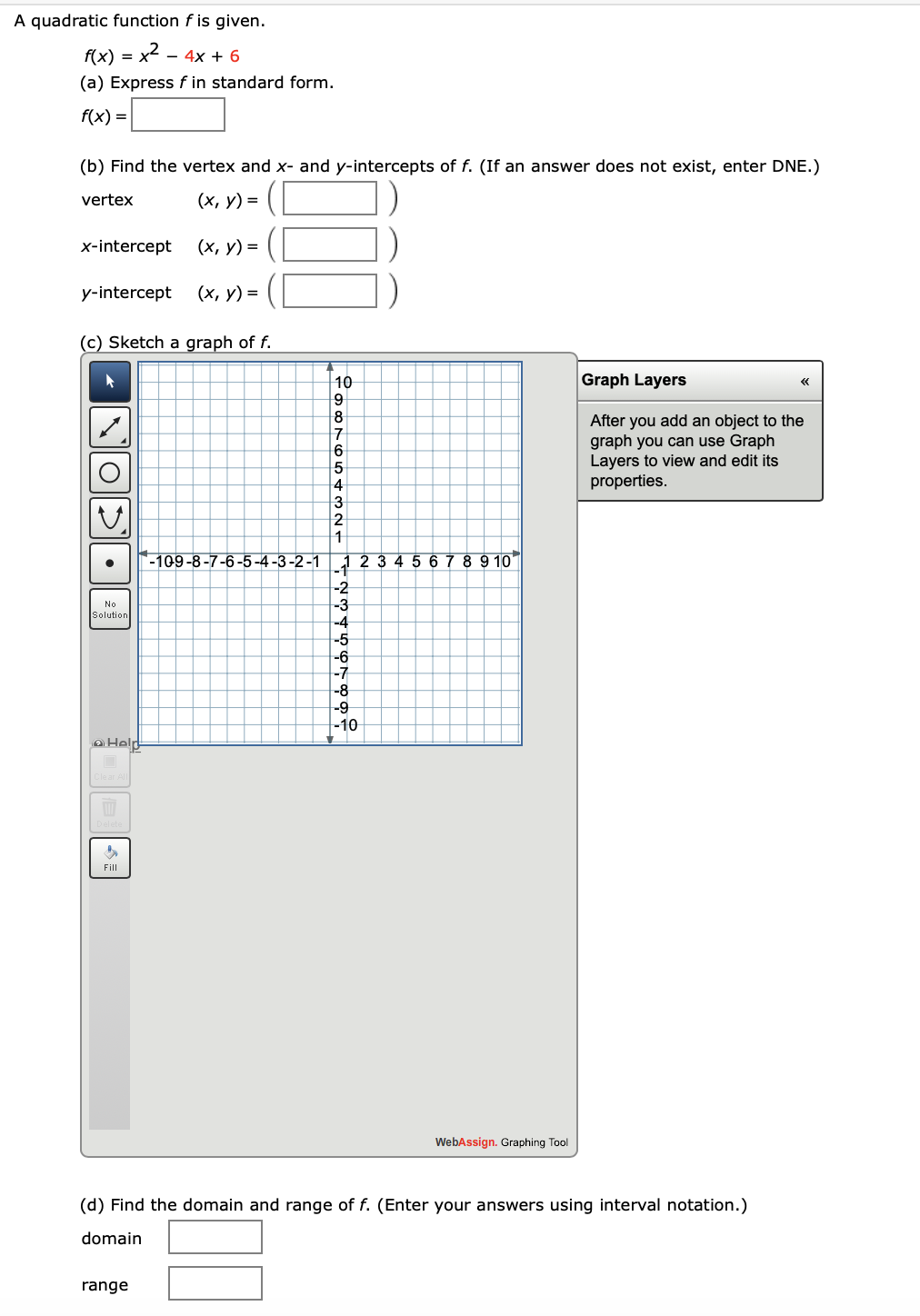



Answered A Quadratic Function F Is Given F X Bartleby



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 p2 unit 2 2 note packet lg 1019 complete lt 8 to end Pdf




Vertex Intercept And Standard Form Ck 12 Foundation
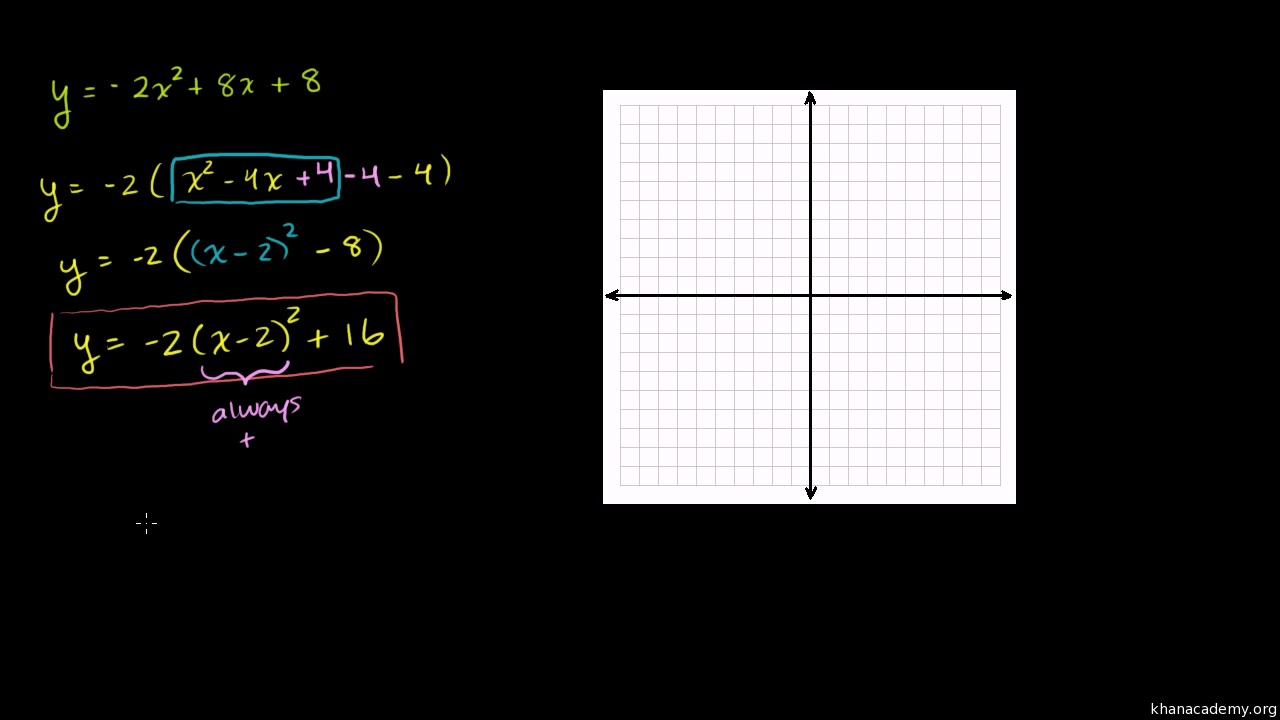



Vertex Axis Of Symmetry Of A Parabola Video Khan Academy
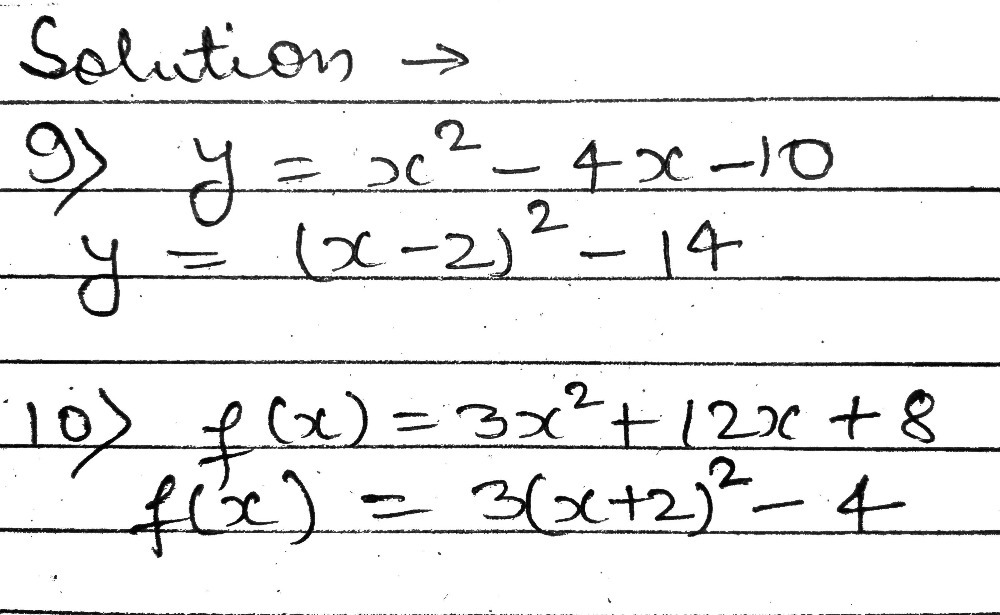



9 Transform Y X2 4x 10 Into The Form Y Ax H2 K A Gauthmath




What Is The Vertex Form Of Y X 2 5x 14 Socratic



Parabolas



Solution Solve By Vertex Form Y X 2 6x 12 Y 4x 2 24x 11



Vertex Form Of Quadratic Equation Mathbitsnotebook Ccss Math



5 2 Quadratic Functions Mathematics Libretexts



What Are The Coordinates Of The Vertex For F X X 4x 10 Quora



1




Ppt 3 7 Warm Up Powerpoint Presentation Free Download Id




1 3 Maximum Or Minimum Of A Quadratic Function Investigate A Pdf Free Download




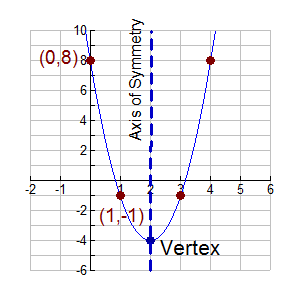
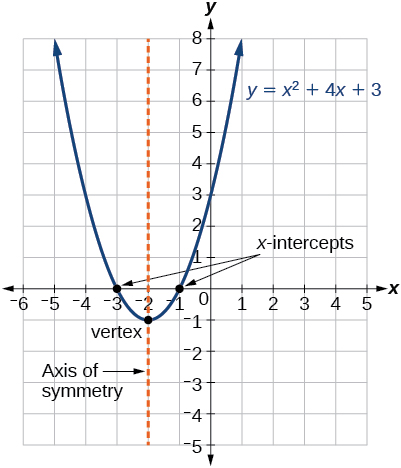
Characteristics Of Parabolas College Algebra




Vertex Form Of Parabolas Use The Information Provided Chegg Com




Complete The Square Lesson Ppt Download
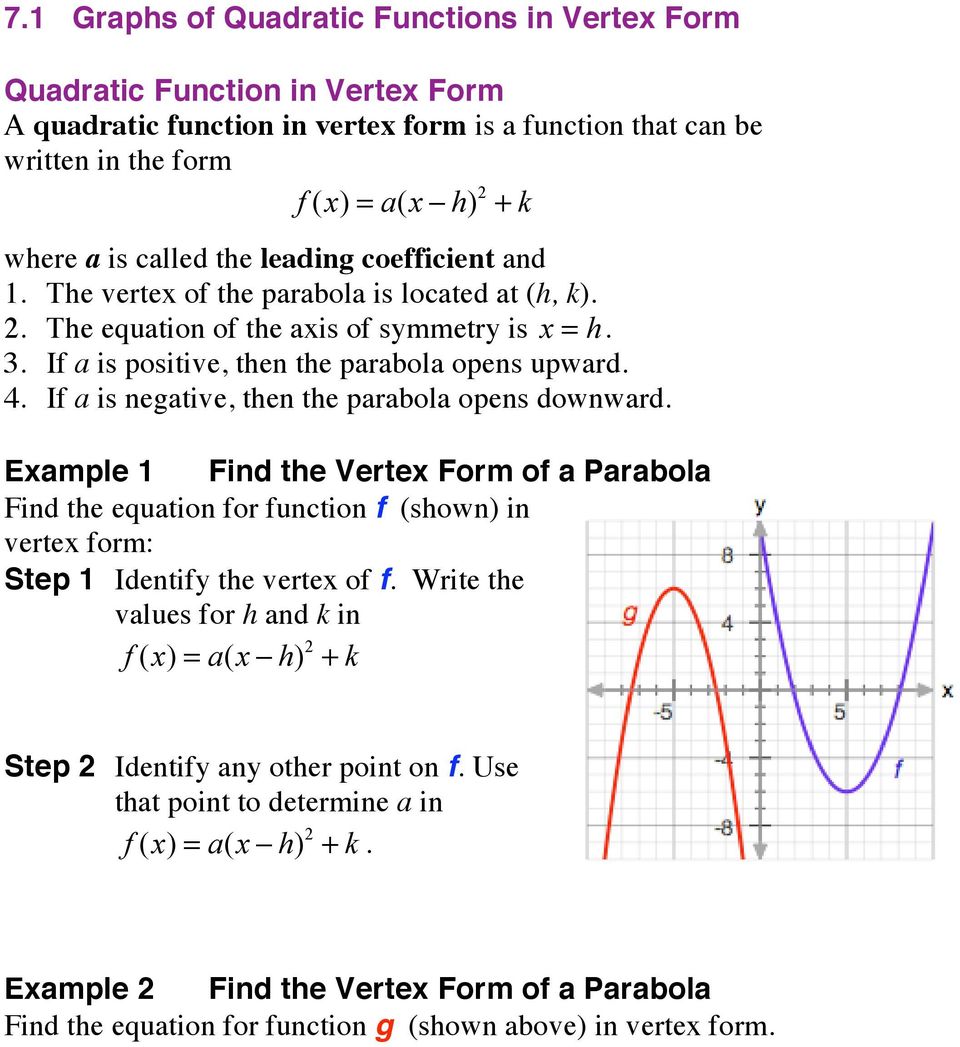



7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download




Finding The Vertex Of A Parabola In Standard Form Video Khan Academy




Write Y X 2 4x 6 In Vertex Form Name Vertex And Axis Of Symmetry Graph Quadratic Function Youtube




Use Completing The Square To Rewrite Y X 2 4x 13 In Vertex Form Identify The Maximum Or Minimum Brainly Com
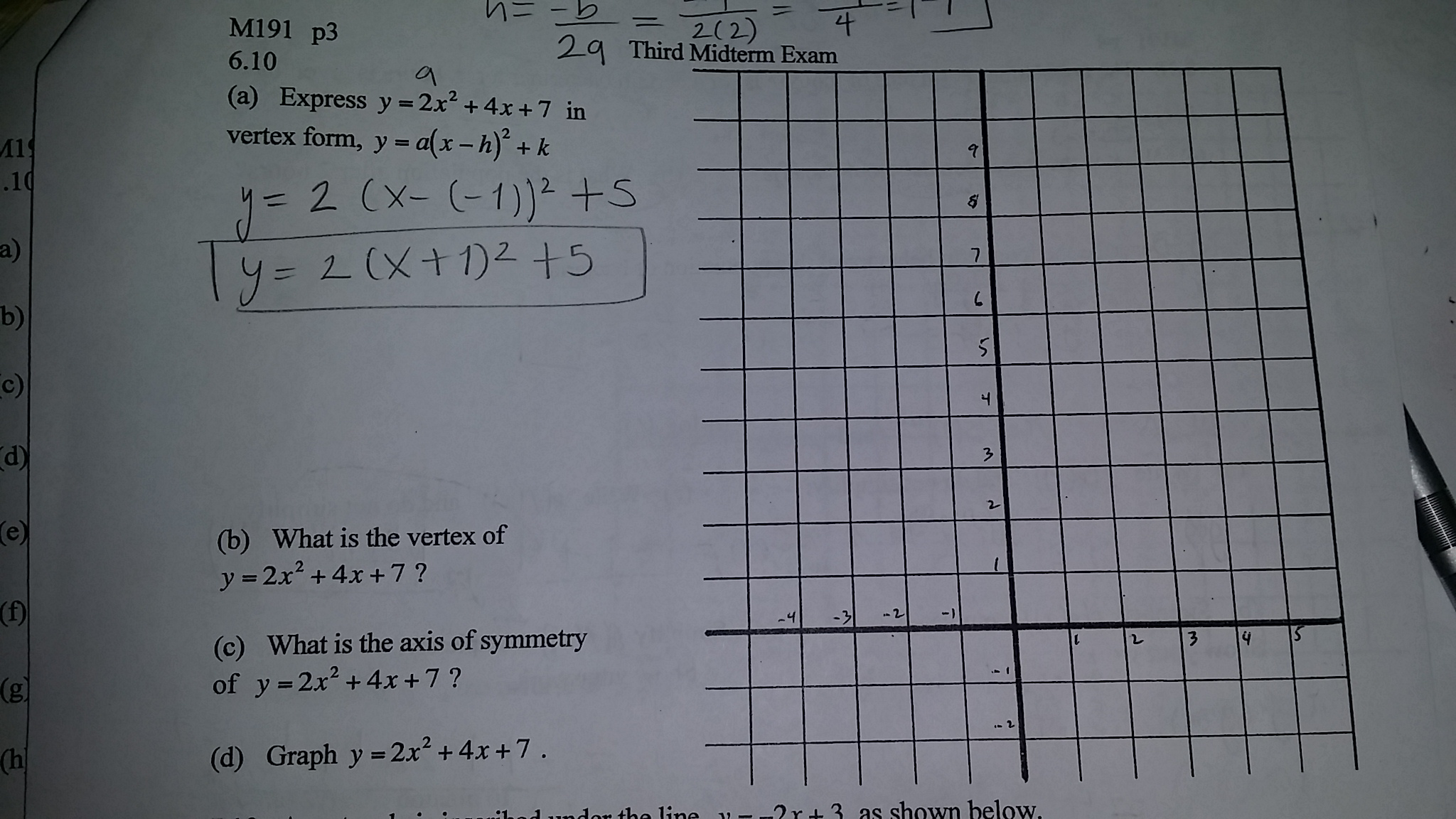



A Express Y 2x 2 4x 7 In Vertex Form Y A X H 2 Chegg Com



Http Pshs Psd2 Org Documents Lnorco Pdf




Fireworks From Standard To Vertex Form Ppt Video Online Download



1




Complete The Square To Rewrite Y X2 4x 5 In Vertex Form Then State Whether The Vertex Is A Brainly Com



Solution How To Get The Quadratic Intercept Form Converted To The Quadratic Vertex Form In The Equation Y 4 X 1 X 6




7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip
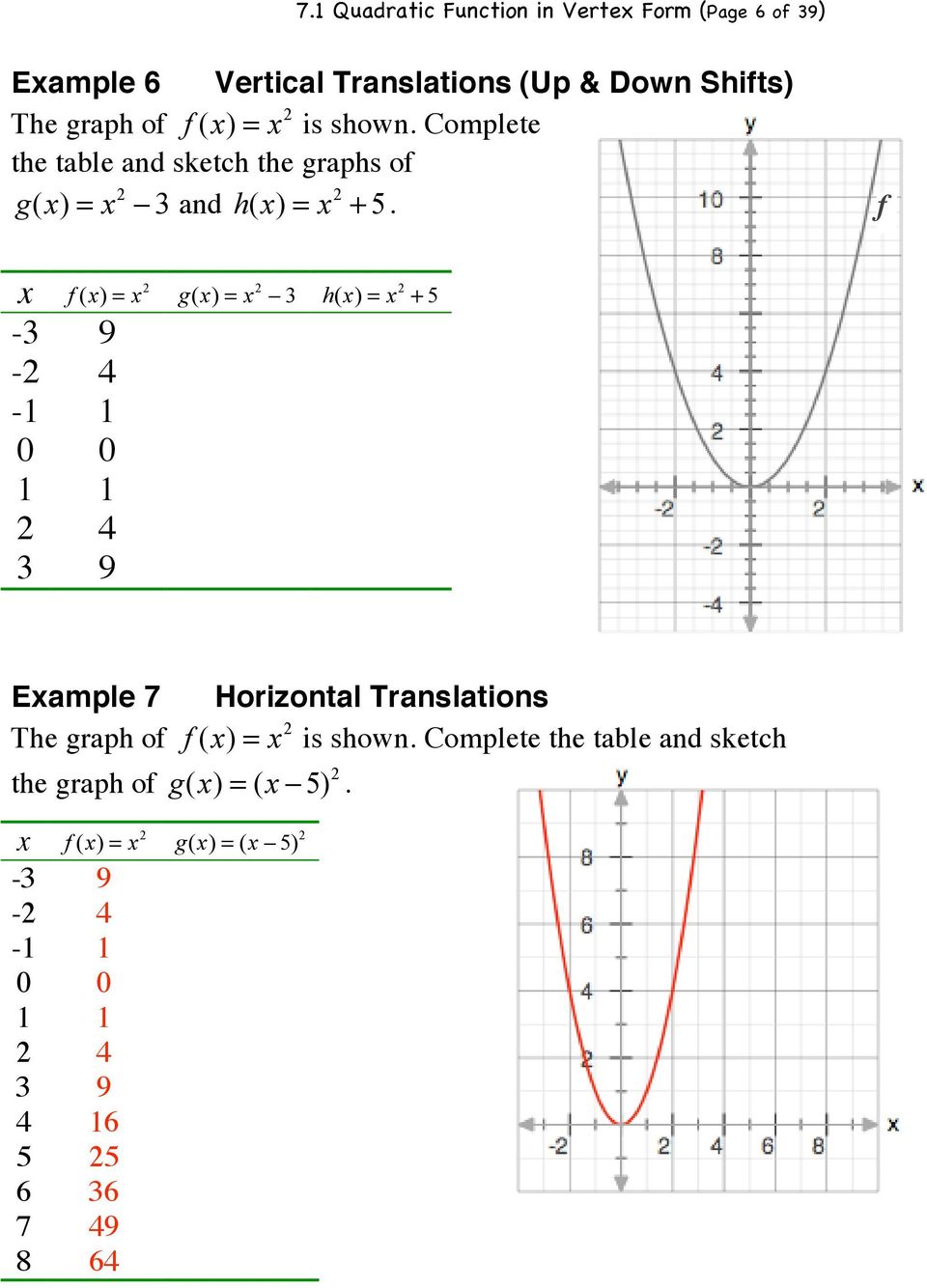



7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download




Chapter 5 Study Guide



Vertex Form Of A Quadratic Equation Algebra Socratic




Ppt Ch8 Quadratic Equation Solving Methods Powerpoint Presentation Free Download Id




4 7 Write In Vertex Form
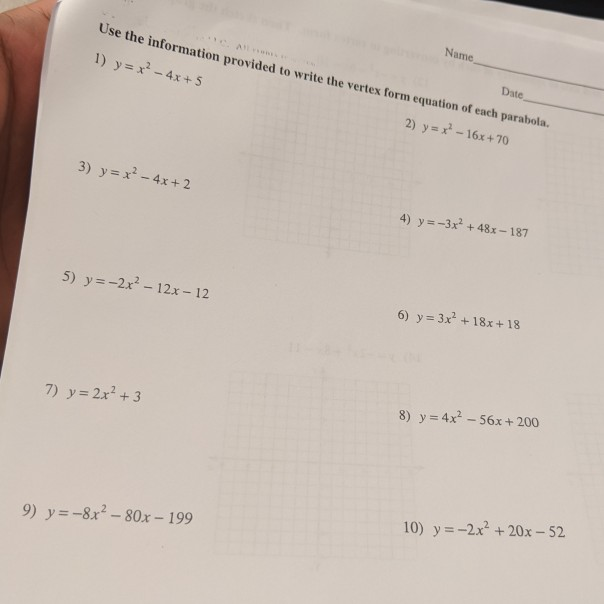



Use The Information Provided To Write The Vertex Form Chegg Com



Http Www Tatecountyschools Org Userfiles 157 Classes 850 A3 review for test 3a Pdf Id




13 The Following Quadratic Function Is Written In General Form F X X2 6x 7 A Write The Factored Form Homeworklib




Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




How Do You Find The Vertex Of Y 2x 2 4x Socratic




Vertex Axis Of Symmetry Of A Parabola Video Khan Academy



What Would An Equation For A Quadratic Function In Vertex Form With Vertex 1 6 That Passes Through The Point 3 4 Be Quora




Y Classzone




3 Vertex Form




Vertex Form Of A Quadratic Equation Doodle Graphic Organizer By Algebrasaurus




Quadratic Equations And Quadratic Functions On The Sat



Solution Write Each Function In Vertex Form Sketch The Graph Of The Function And Label Its Vertex 33 Y X2 4x 7 34 Y X2 4x 1 35 Y 3x2 18x 36 Y 1 2x2 5x




Quadratic Equations And Quadratic Functions On The Sat



2 2 Characteristics Of Quadratic Functions Flip Ebook Pages 1 10 Anyflip Anyflip




4 6 Completing The Square Completing A Perfect Square Trinomial Allows You To Factor The Completed Trinomial As The Square Of A Binomial You Can Solve Ppt Download




Quadratic Functions
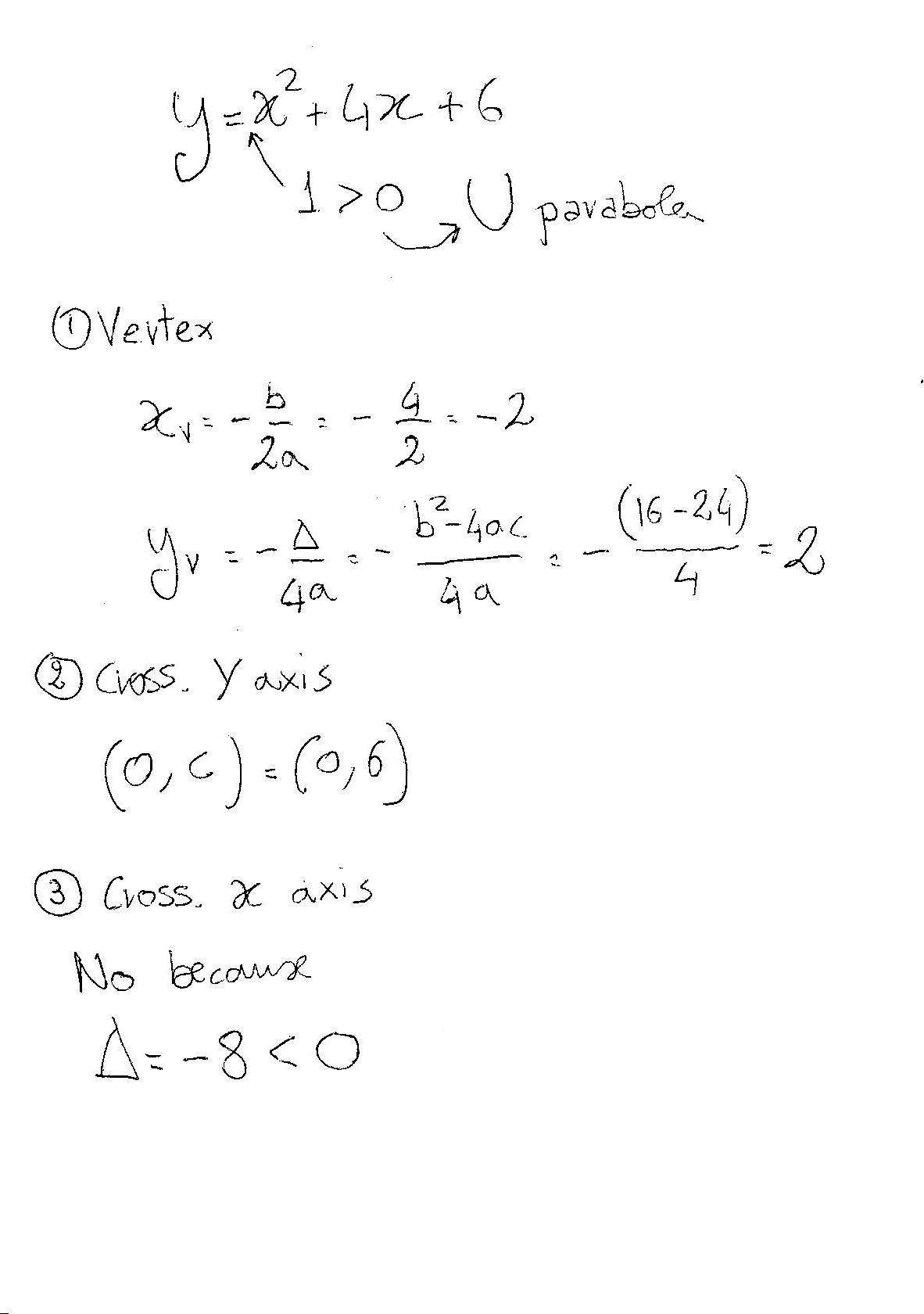



How Do I Graph The Quadratic Equation Y X 2 4x 6 Socratic




Example 6 Write A Quadratic Function In Vertex Form Write Y X 2 10x 22 In Vertex Form Then Identify The Vertex Y X 2 10x 22 Write Original Ppt Download



Learn How To Convert To Vertex Form By Completing The Square And Then Graph Y X 2 4x 7 Youtube




Math 2 Warm Up 2x2 4x 3x 5 3x X 2 X 2 X 5 Ppt Download




Ppt 3 7 Warm Up Powerpoint Presentation Free Download Id



Vertex Form Of A Quadratic Equation Algebra Socratic



How To Write The Vertex Of The Parabola Y X 2 8x 10 Quora



Solution In The Box Complete The First 4 Steps For Graphing The Quadratic Function Given Use On The Keyboard To Indicate An Exponent Then Print A Sheet Of Graph Paper And




What Is The Vertex Form Of Y X 2 16x 71 With Steps Please Brainly Com
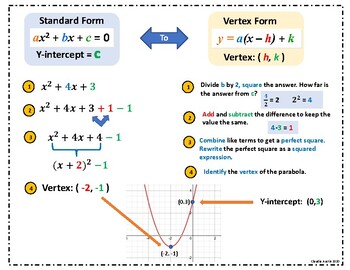



Quadratic Equation From Standard To Vertex Form By Claudia Austin




7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download




Vertex Form Vertex Form Vertex Form Is Another



Search Q Completing The Square Tbm Isch




Converting Quadratics Vertex Form To Standard 13 Write An Equation For A Parabola With Vertex Pdf Document




Vertex Form Of Parabolas Kuta Software



Graphing Quadratic Functions




Write Each Function In Vertex Form Y X 2 4x 6 Homework Help And Answers Slader




Standard Form To Vertex Form Definitions Facts And Solved Examples Cuemath




Quadratic Equations And Quadratic Functions On The Sat



0 件のコメント:
コメントを投稿