具体例で学ぶ数学 > 図形 > 円柱の表面積と体積を求める公式 最終更新日 円柱の体積 V は、 円周率× 半径 × 半径 × 高さ 円柱の表面積 S は 2 ×円周率× 半径 × 半径 + 2 ×円周率× 半径 × 高さ このページでは、円柱の表面積について詳しく説明 第14問 三角すいの表面積 図形ドリル 6年生 三角すい 展開図 立方体 表面積 ★★★★★☆(算オリ・灘中受験生レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。π (cm 2 ) 側面は長方形で,縦の長さが8cm,横の長さは底面の円周の長さに等しい 側面の長方形の横の長さは8× π cm,縦の長さは8cmであるから,側面積は64 π (cm 2 ) (答) A B C D 立体は円柱になり,表面積は底面積×2=16 π ×2 (cm 2 )と側面積8 π ×7 (cm 2 )の合計になります 底面積2つで32 π (cm 2 ),側面積56 π (cm 2 )の合計は π (cm 2 ) (答) ※以下,8番以後の問題を解くに
攻玉社11 5 の 1 立体図形 立方体を平面で切断したときの体積と表面積 気まぐれ解説カフェ 仮
立方体の表面積 公式
立方体の表面積 公式- 切断された立方体の表面積(桜蔭 08)切り取られた円柱(sapix7月入室、組分けテストより)直方体の切断(四谷大塚 合不合判定予備テストより)立方体の切断(慶應義塾中等部 受験算数問題 00年)立方体の切断回数(横浜共立学園中学 受験算数問題 08年)立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)



攻玉社11 5 の 1 立体図形 立方体を平面で切断したときの体積と表面積 気まぐれ解説カフェ 仮
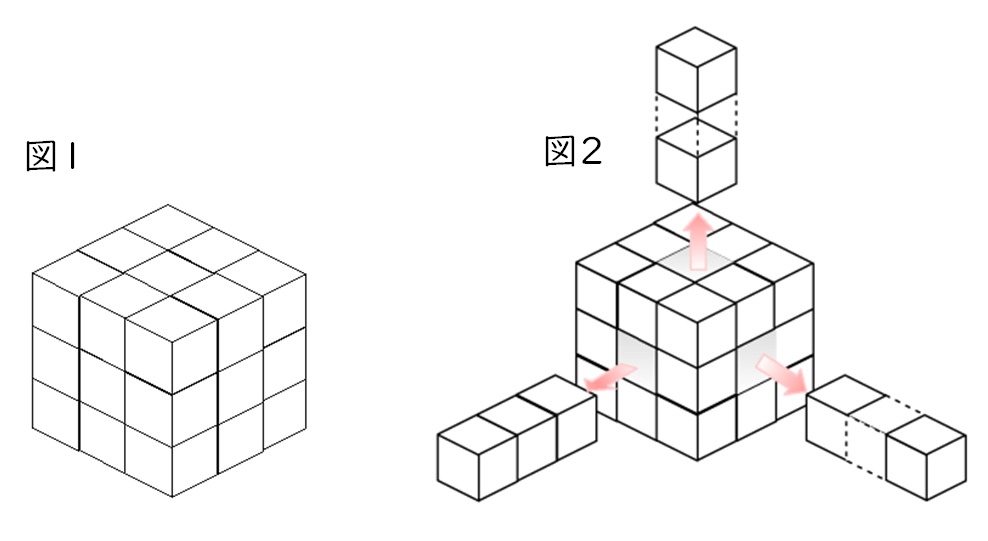
立方体のような立体 立方体のような物体に付いている灰色部分の面積はいくらか. この物体を一辺が の立方体に入れる. 円の半径=立方体の一辺の半分= (左図) 斜めの線= (三平方の定理)(右図) 上図の① ②=① ②の線=赤い三角形の一辺を 15個の立方体(一辺が1 cm)を組み合わせてできる立体について,表面積は何cm2ですか。 PDFファイルをダウンロード 問題の答え合わせをTwitter上で随時受け付けております。 立体の表面積の計算ドリル 概要 立体の表面積についての問題です。 経過 10年9月6日 はじめにアップしたのは、1辺1cmの立方体を平面状につなぎ合わせた立体についての問題です。
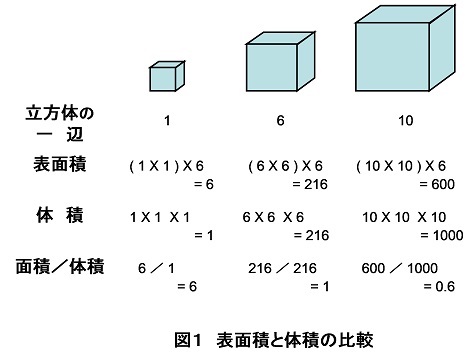
立方体の12の辺の長さは等しく、これを $a$ とします。立方体の表面積 $S$ は、次の式で求められます。 立方体の表面積 \begin{align*} V = 6a^2 \end{align*} 表面積 = 一辺 × 一辺 × 6立方体の表面積sは「一辺の長さの2乗に6を掛けた値」です。 公式はS=6a 2 です。 直方体の表面積Sは「S=2ab2ac2bc」で計算できます。半径が同じrであるとき、次元を上げてゆくと表面積は七次元球が、体積は五次元球が最大になることがわかっています。 立方体ではどうでしょう。 一辺をaとするとき 二次元正方形の周囲は4a、面積はa² 三次元立方体の表面積は6a²、体積はa³です。
体積を入力し「立方体の1辺・表面積を計算」ボタンをクリックすると、立方体の1辺の長さ・表面積を計算して表示します。 体積 V: 体積Vが8の立方体の1辺の長さ・表面積 展開図(直方体・立方体):重なる点・平行な辺と面 積み重ねられた立体①:表面積と体積! 投影図→見取り図のテクニック2つ!(積み重ねられた立体②) 積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)立方体の一辺の長さを入力 一辺 = 54 立方体の体積 v = 立方体の表面積 s = このように入力した一辺の長さに対する体積と表面積を計算してくれます。



この問題教えてください くり抜く前の立方体の表面積は64ですか Yahoo 知恵袋



攻玉社11 5 の 1 立体図形 立方体を平面で切断したときの体積と表面積 気まぐれ解説カフェ 仮
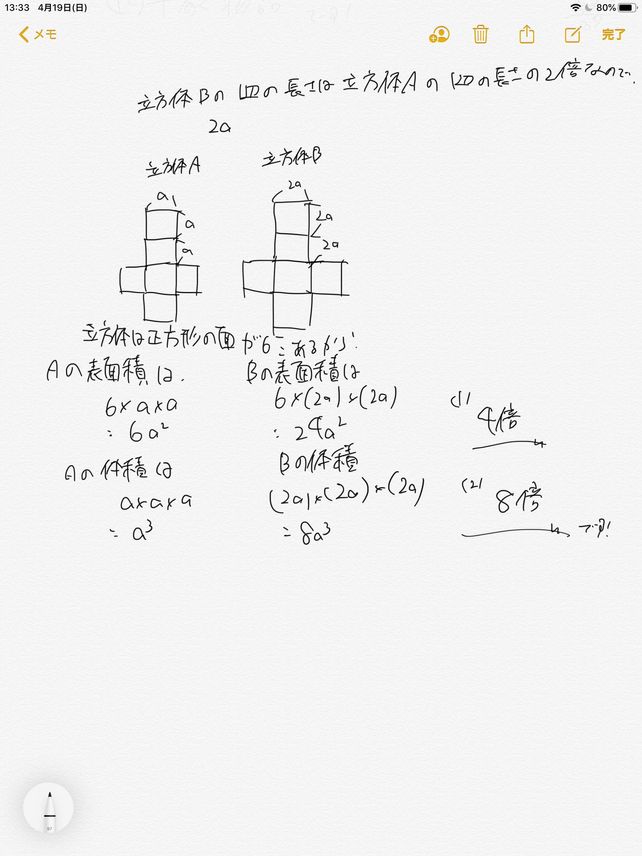
問題『1辺が a cm の立方体と、その各辺を k 倍した立方体があります。これらの立方体の表面積の比と体積の比をそれぞれ求めなさい。』について、 太郎さんは、面積の比を 1: k 2 、体積の比を 1: k 3 と答えました。体積・表面積 練習問題 Hello School 算数 体積・表面積 練習問題 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 ※特に指定がない場合、円周率は314とします。 1. アの体積は128cm3、イの体積は2512cm3です。 それぞれの立体の の値を求めなさい。 ア イ立方体の表面積は次の公式(一辺の長さをaとしている)で求めます。 a × a × 6 6という数は、立方体が6枚の正方形に囲まれていることを意味します。 計算例 一辺が 1cm の立方体 表面積 = 1 × 1 × 6 = 6cm 2 一辺が 2cm の立方体 表面積 = 2 × 2 × 6 = 24cm 2 一辺が




この問題の解き方を教えてください Clear



1
デスクトップPC 体積を微分すると・・・ 球の体積を微分すると表面積になるが、立方体の体積では?のようなことが話題になっているホームページを知っている方いませんでしょうか?どうなるかはわかっている 質問No 立方体の積木の場合、表面積は「3方向の面積の和×2 」で求められますが、凹みがある場合は少し注意が必要です。 投影図(推理) 投影図から得られる情報は完全ではないことがあります。 中学受験算数問題(立体のくりぬき)立方体のくりぬき(ラ・サール中学 受験算数問題 09年)穴あき立方体(中学受験算数 中が見えない問)表面積の差(成蹊中学 10年)くり抜いたあとの表面積(須磨学園中学 10年)くり抜かれた立体の体積(鴎友学園女子中学




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




表面積の求め方 計算公式一覧
体積・表面積の計算 ・立方体の体積・表面積 ・立方体の体積から1辺 ・立方体の表面積から1辺 ・直方体の体積・表面積 ・直方体の1辺・表面積 ・直方体の1辺・体積 ・正四面体の体積・表面積 ・正四面体の体積から1辺 ・正四面体の表面積から1辺辺の長さをすべて同じなので、同じ正方形6つで囲んだものとなります。そのため、ひとつの正方形の面積を6倍すれば立方体の面積を求めることができます。つまり計算方法は 辺の長さ×辺の長さ×6 となります。 立方体の表面積を求める公式2 比表面積の定義および粒子径との関係 比表面積は一般に単位重量の粉体中に含まれる全粒子 の表面積の総和Sw(cm2/g)で 表わすが,単 位体積あた りの全表面積S,(cm2/cm3)で 示すこともある。ここで 単位体積というのは粉体の見掛けの体積(か さ)で はな



立方体の個数と表面積 共立女子中学 2010年 どう解く 中学受験算数




モノコミュニティ 採用情報
緑色の直方体のうち小さい方は下部のどこにあってもよい。 この立体の表面積は、 12×12×2+13×12×4+12×2+11×2+2=2+624+24+22+2=960 から、960cm2で、らすかるさんの答えと一致する! らすかるさんによれば、12×13×13-18 でも 12×12×14-6 でも同じになると のこと。 (コメント) mita さん、らすかるさんに感謝します。 当HPがいつもお世話になってMixi数学科 教師 講師 積み木図形の表面積の最小化 問 1辺の長さが1cmの立方体が10個ある。これらの立方体の面と面をずらさずにくっつけていき,1つの連結な立体を作る。 このとき,作ることのできる立体の表面積の最小値が30cm^2であることを証明せよ。球の表面積が直径を通る円の面積の4倍であることを知っていることが前提ですが、 円の面積は外接する正方形の面積のおよそ4分の3 立方体の表面積は円に外接する正方形の6つ分 球の表面積は円の面積の
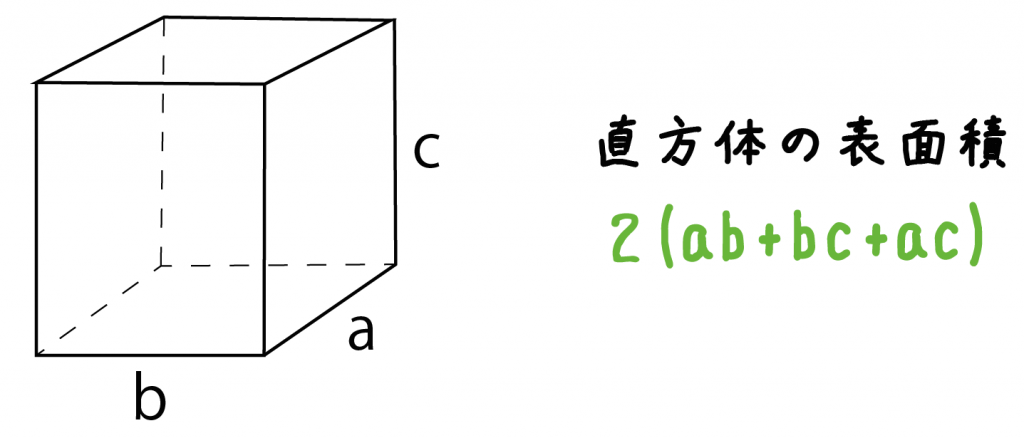



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




スタディピア 立体の表面積
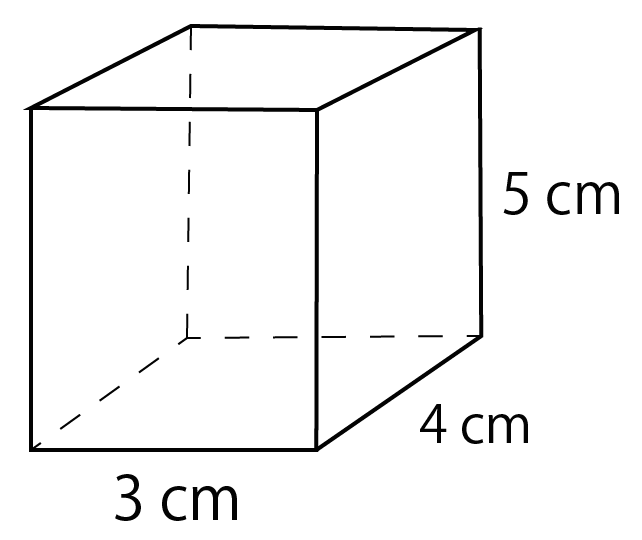
直方体の縦・横・高さを入力 縦 = 34 横 = 52 高さ = 41 直方体の体積 v = 724 直方体の表面積 s = 1050 このように入力した縦・横・高さに対する体積と表面積を計算してくれます。粒子の形状が球の場合は, φ v = π/6,φ s = π であり,立方体なら φ v = 1,φ s = 6 (ただし,立方体の1辺を D p として) となる.φ v および φ s は,同じ粒子でも,粒子径 D p のとり方によって異なってくる.また,粒子の単位体積当たりの表面積47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。




小5 算数 小5 3 直方体と立方体の体積 Youtube




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
一辺129 Mmの立方体の表面積 半径1784 Mm(直径3568 Mm)の円の面積 半径2 Mm(直径1784 Mm)の球の表面積 765 × 10 15 m 2 海王星の表面積 813 × 10 15 m 2 天王星の表面積 10 16 10 000 Mm 2 10 000 Mm 2 一辺100 Mmの正方形の面積 一辺408 Mmの立方体の表面積



図の立体の表面積を求めなさい という問題です 元の立方体の表面積は出せま Yahoo 知恵袋



数学 球の表面積を積分で計算してもうまくいかない人へ



ホルスタイン と ベルクマンの法則 との関係 酪農後継者のためのdairy Guide



Enaシンガポール校 Ena国際部




5 3 対角線から立方体の体積 表面積を求めるには さんすうがく
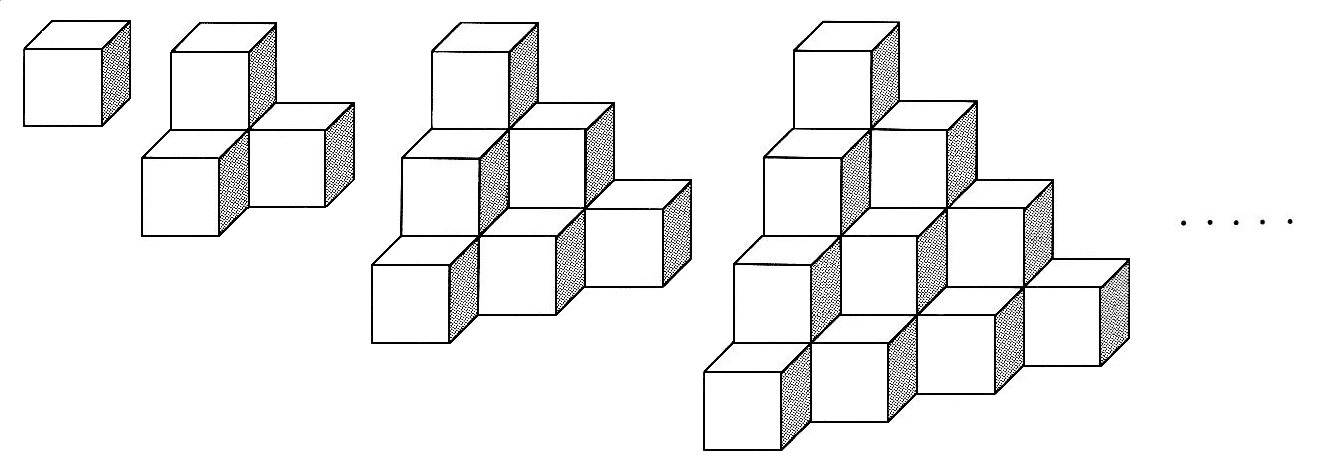



北辰塾 情報局 直撃 中学入試問題 第230回 青学英和 立体 立方体の積み重ね



穴のあいた立体の表面積 浦和明の星女子中学 2012年 どう解く 中学受験算数



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方




計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



4次元物体の表面積はどうやって計算するのですか Quora



湘南白百合11 5 立体図形 立方体を切断してできる立体の体積や表面積 気まぐれ解説カフェ 仮



Math 積み重ねた立方体の表面積 働きアリ




切断面のある立体の表面積 算数の問題 身勝手な主張
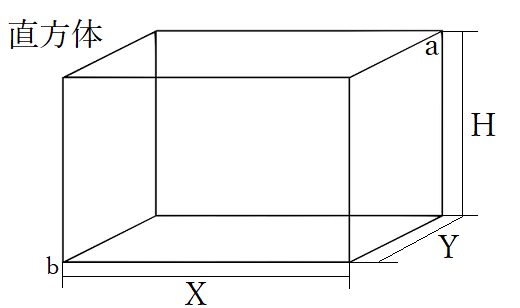



直方体の体積 表面積 対角線 計算機 かんたん計算機
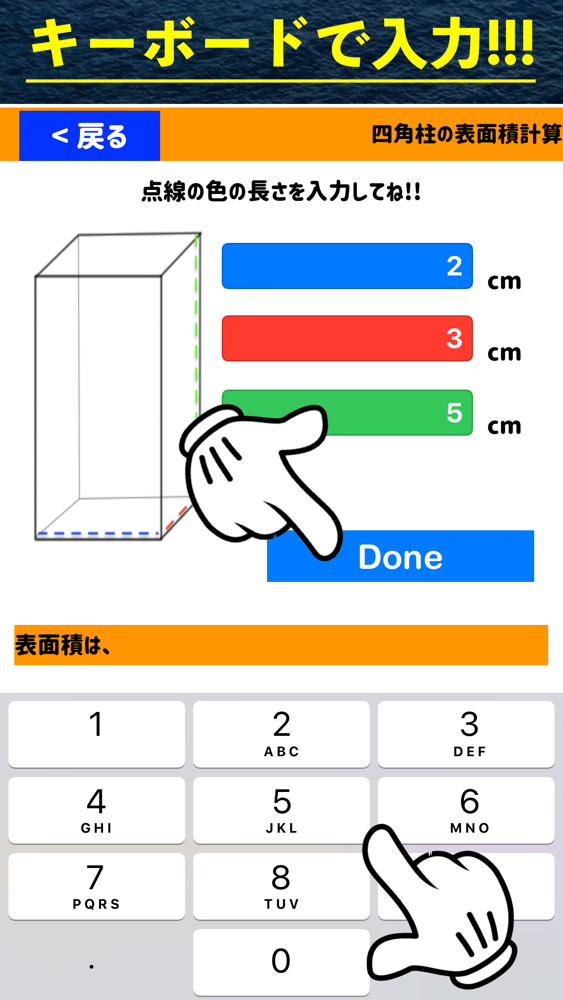



立方体の表面積計算電卓アプリ App For Iphone Free Download 立方体の表面積計算電卓アプリ For Ipad Iphone At Apppure
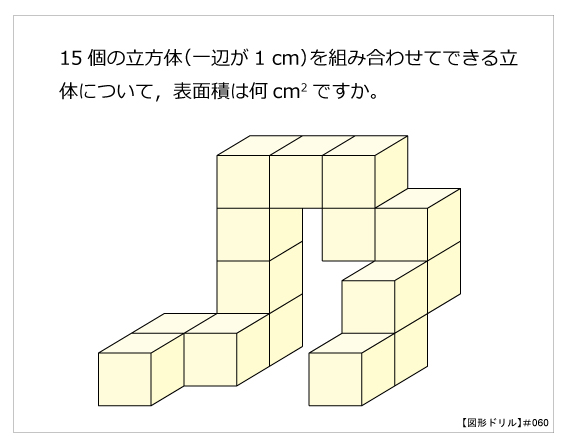



図形ドリル 第60問 立方体の表面積 算数星人のweb問題集 中学受験算数の問題に挑戦




3cm Kabcd Efgh A B See How To Solve It At Qanda



表面積 中学受験ー算数解き方ポータル



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方
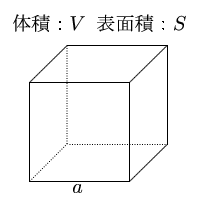



立方体の体積 表面積 体積 表面積の計算 計算サイト




計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




Y X Nの微分の意味 Geogebra




Newみんなの算数講座33 直方体の表面積を小さくする 中学受験の算数知恵宝庫
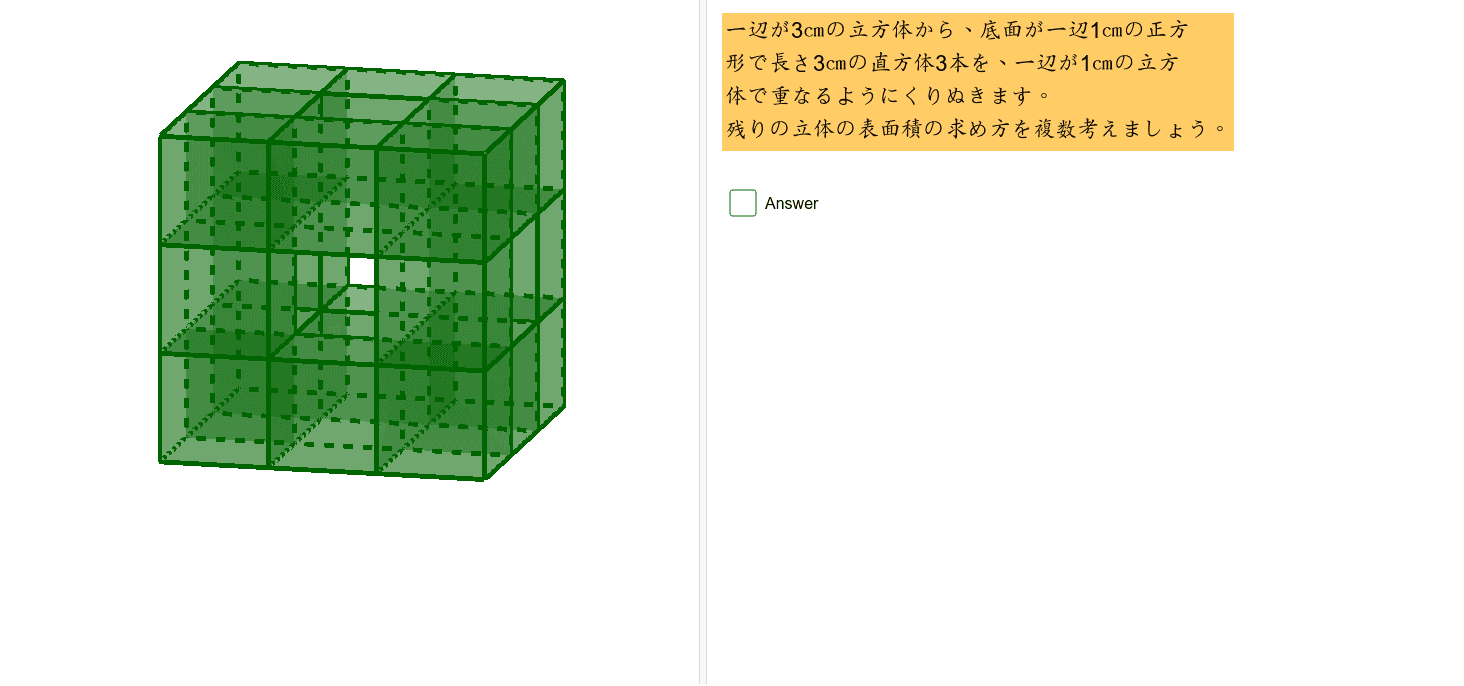



くりぬき立方体 表面積 Geogebra
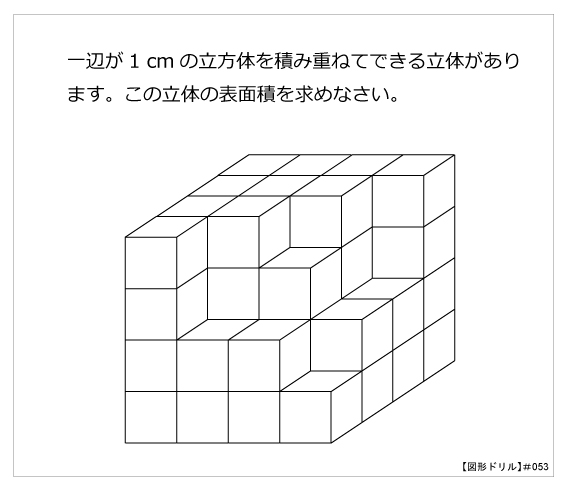



図形ドリル 第53問 立方体と表面積 算数星人のweb問題集 中学受験算数の問題に挑戦




ボード 勉強法 のピン
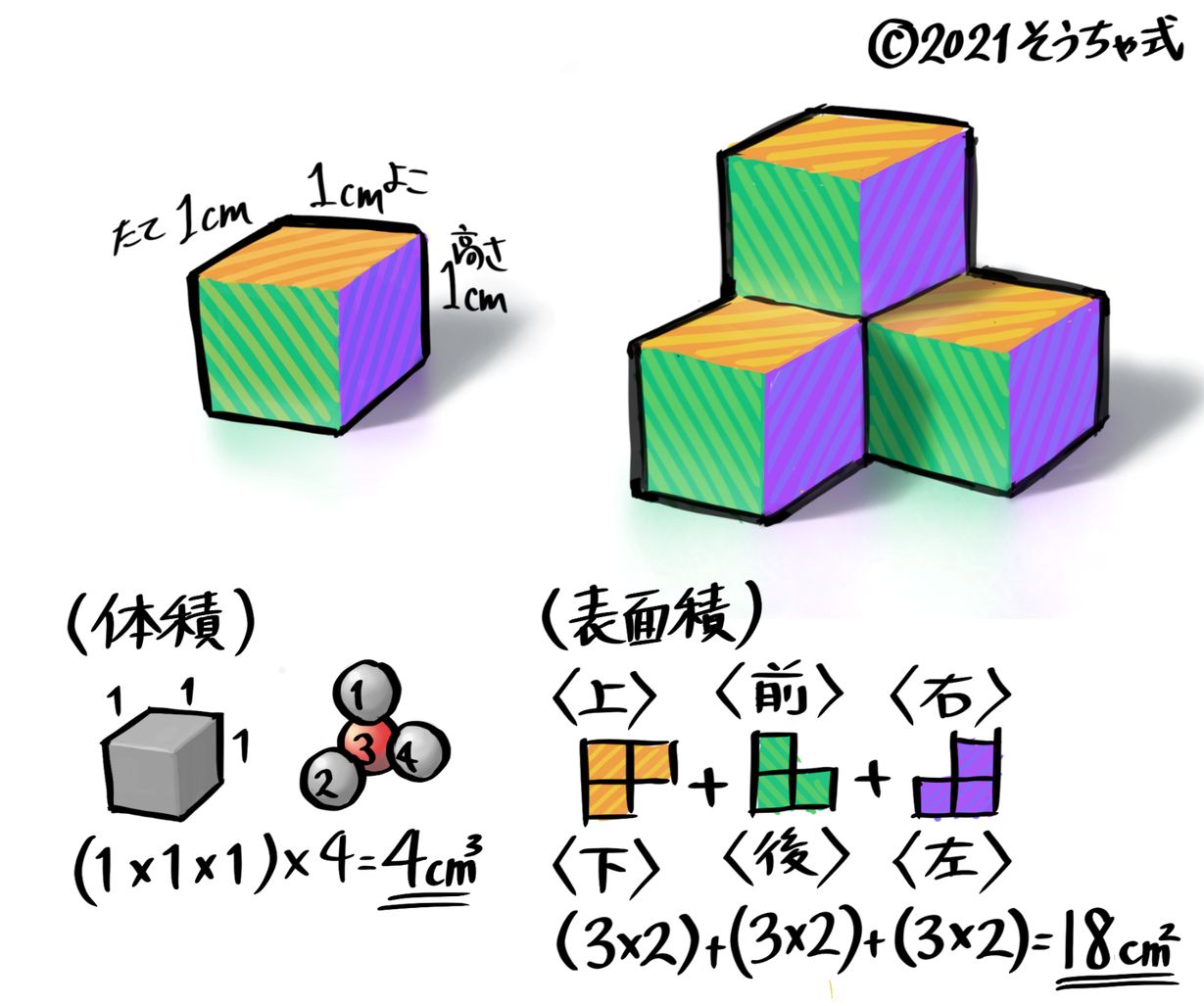



中学受験 直方体 立方体のまとめ 立体図形 そうちゃ式 受験算数 2号館 図形 速さ



App Store 上的 立方体の表面積計算電卓アプリ



図形に強くなる 立方体 中学受験ブログ



Math 積み重ねた立方体の表面積 働きアリ



立方体の表面積計算電卓アプリ Iphone Ipad Game Reviews Appspy Com



5 5 複雑な立体の表面積と面積を求めるには さんすうがく
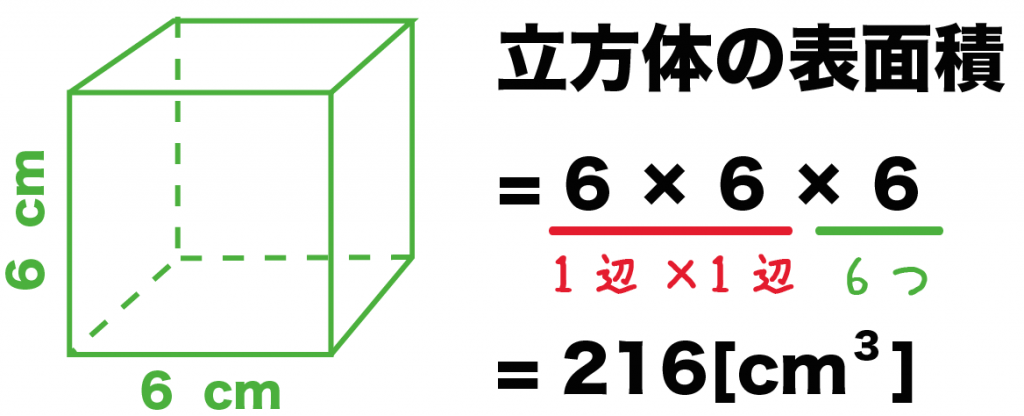



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



1




立体の表面積 小学生算数です教えて下さい Okwave
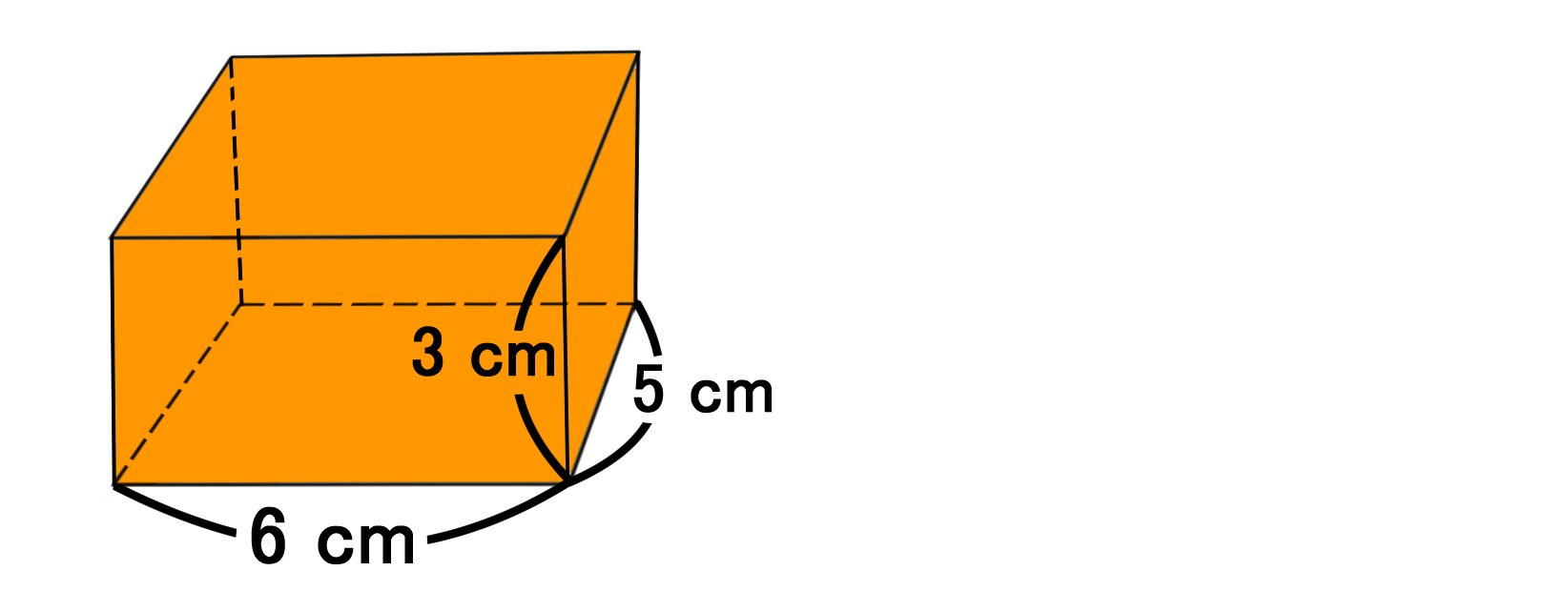



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




表面積の求め方 計算公式一覧




1 6cm Descubre Como Resolverlo En Qanda




スタディピア 立体の表面積




表面積と体積の不思議な関係 qazのつれづれ日記



Updated 立方体の表面積計算電卓アプリ Pc Iphone Ipad App Download 21



Newみんなの算数講座102 穴をあけると表面積は増える 中学受験の算数知恵宝庫
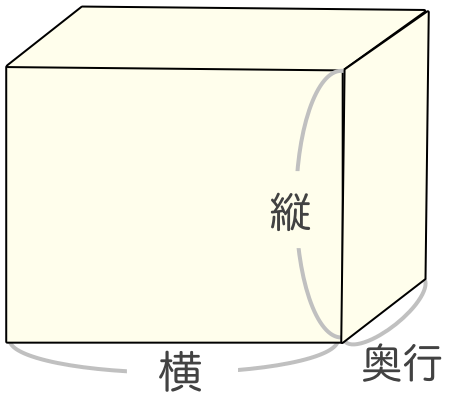



直方体の表面積 簡単に計算できる電卓サイト



Updated 立方体の表面積計算電卓アプリ Pc Iphone Ipad App Download 21




立方体と直方体 角柱の表面積 底面積 2 底面の周 高さ ワンセンテンス算数 Note
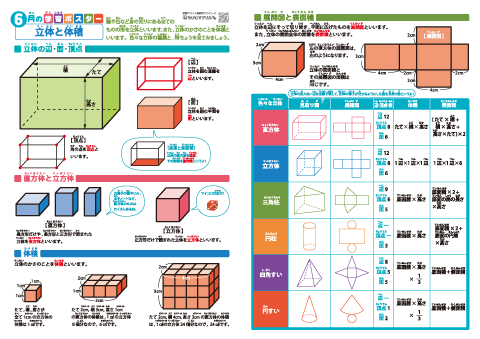



小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム
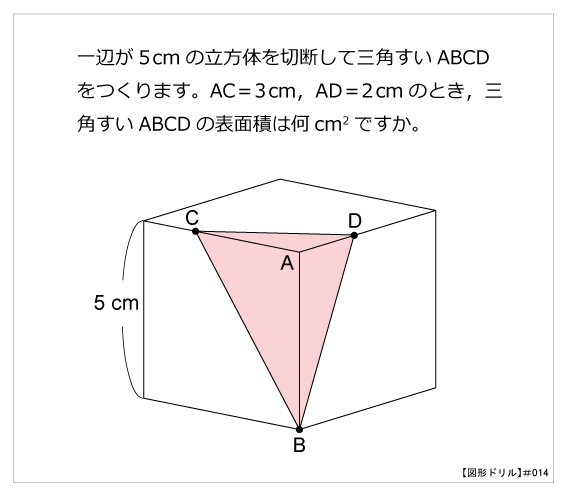



図形ドリル 第14問 三角すいの表面積 算数星人のweb問題集 中学受験算数の問題に挑戦




1 Y 1 3 Y X Y X 2 Descubre Como Resolverlo En Qanda



Math 積み重ねた立方体の表面積 働きアリ




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




立方体の表面積計算電卓アプリ By Takaaki Sasaki



Math 積み重ねた立方体の表面積 働きアリ The 2nd



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1



くりぬき立方体の表面積 聖光学院 H24大問1の3




どうやって解くのですか 解き方を教えてください Clear
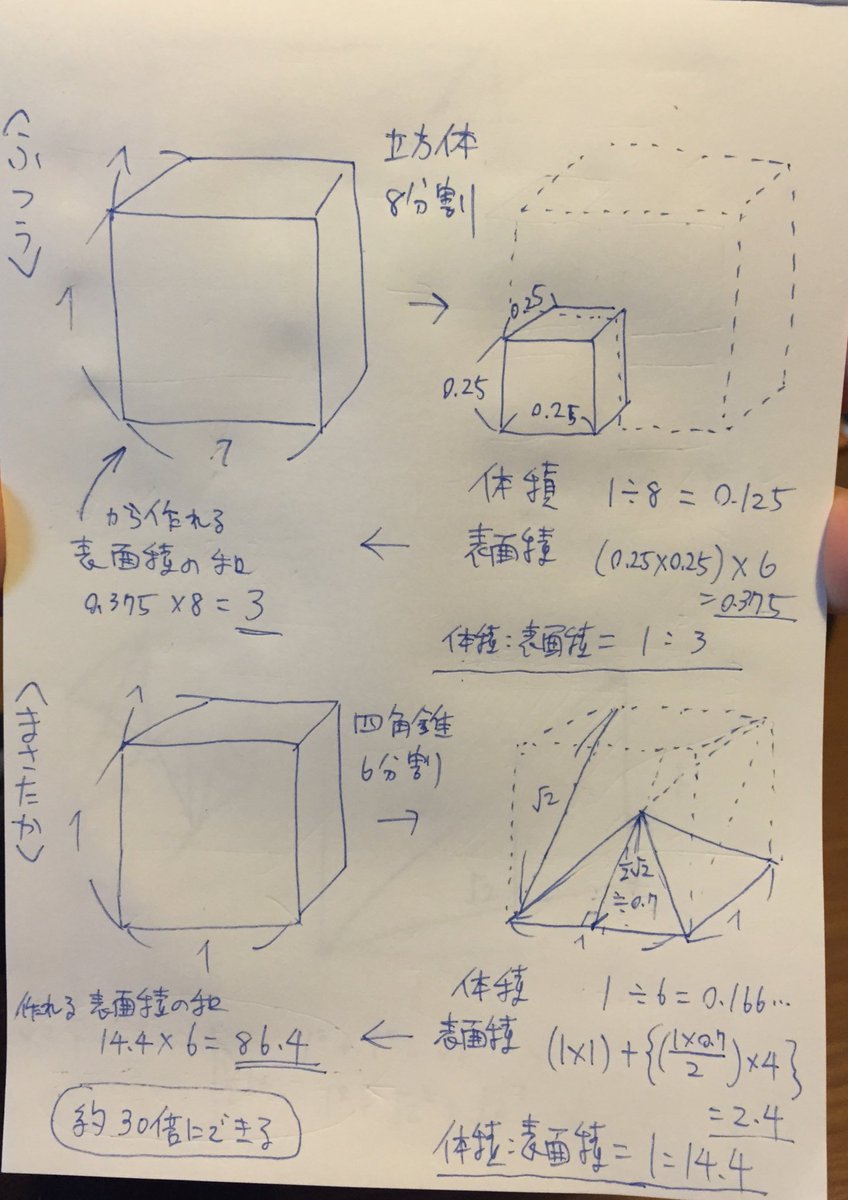



さわやか ワ2nd7 11 再放送bs朝日 もう誰かやってると思うけど 表面積を比較すると 匡貴の割り方は体積 表面積 比を約5倍に 同じ立方体から作れる表面積を約30倍にできるっぽい 計算あってるかな 表面積が威力に効いてくる場合メリットがあるのかも
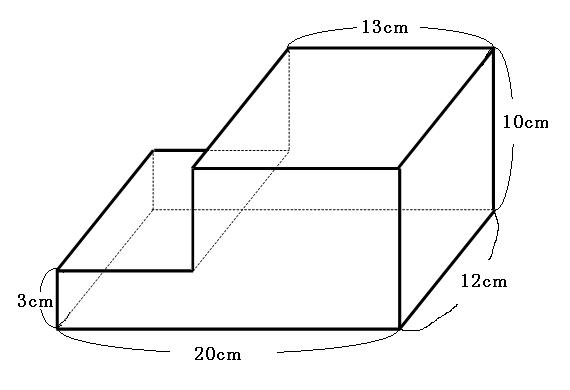



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか
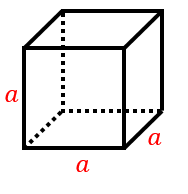



立方体と直方体の表面積を計算する 具体例で学ぶ数学



下の図のような 1辺がacmの立方体がある この立方体の縦を2cm 横を Yahoo 知恵袋
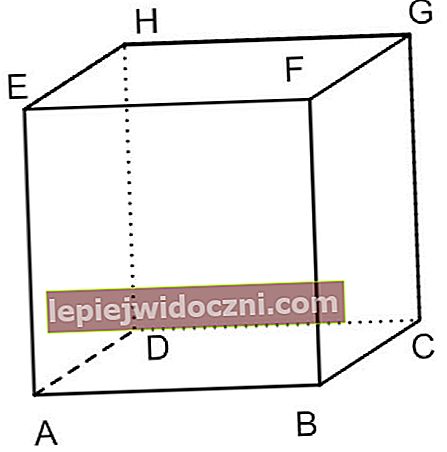



立方体の表面積式と学習する問題の例
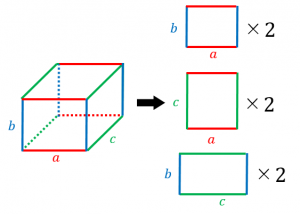



立方体と直方体の表面積を計算する 具体例で学ぶ数学
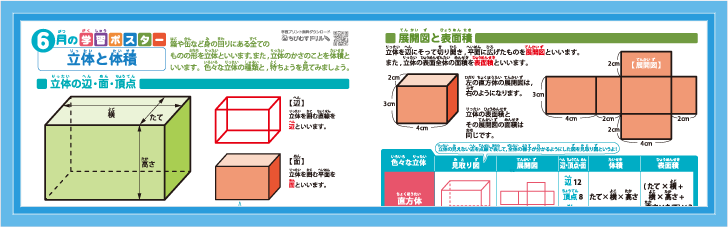



小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習



写真のように 1辺が1cmの立方体を14個積み重ねました この立体 Yahoo 知恵袋




マスラボ 中学受験の基礎知識 直方体や立方体の表面積 Youtube




体積 表面積
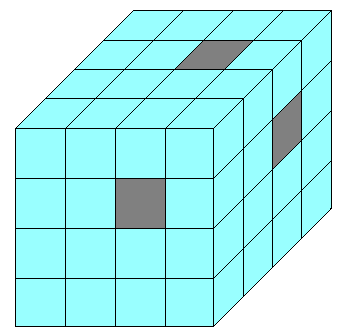



問題113 積み木の問題



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式




中学受験算数 直方体と立方体 体積と表面積 小学4年生 6年生対象 毎日配信 例1 2 の答えに訂正あり 概要欄に記載しております Youtube




スタディピア 立体の表面積



Bar 1 A A 1 1 Descubre Como Resolverlo En Qanda
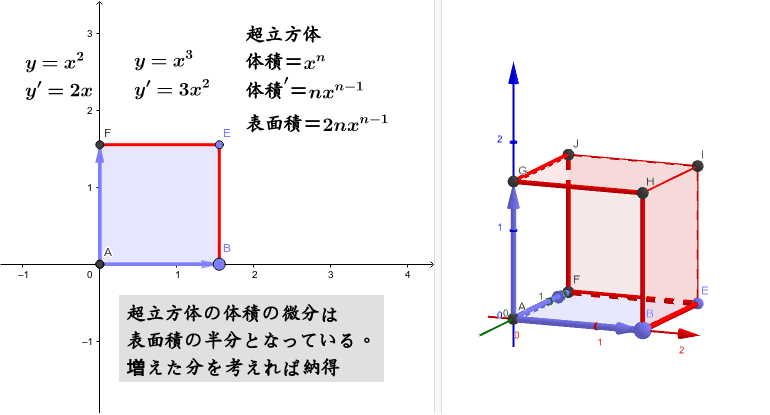



Y X Nの微分の意味 Geogebra




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




立方体の体積と立方体の表面積の式と問題の例



1




15番目の立体の表面積の求め方が分かりません 教えてください Clear




立方体と直方体 直方体を組み合わせた立体の表面積は 足していくか 引いていくか ワンセンテンス算数 Note




表面積問題 以下の画像にある立方体の表面積の求め方を教えてください Okwave
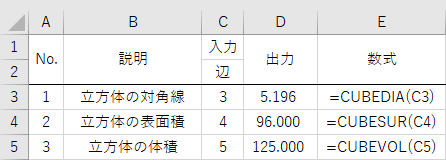



Excel関数 立方体の体積や表面積などを計算するcubeカスタムワークシート関数群 黒い箱の中



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方




Sqrt5 1 Acm 3 Descubre Como Resolverlo En Qanda




算数的分野 くりぬき立方体の表面積




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook
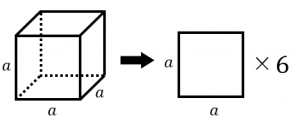



立方体と直方体の表面積を計算する 具体例で学ぶ数学
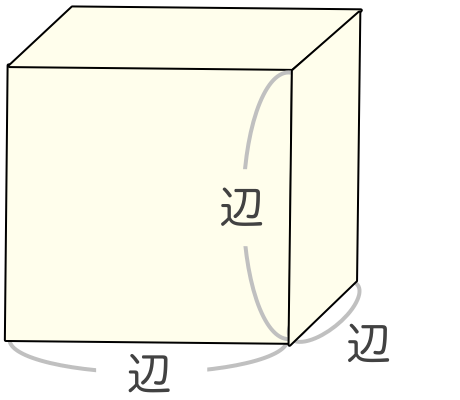



立方体の表面積 簡単に計算できる電卓サイト
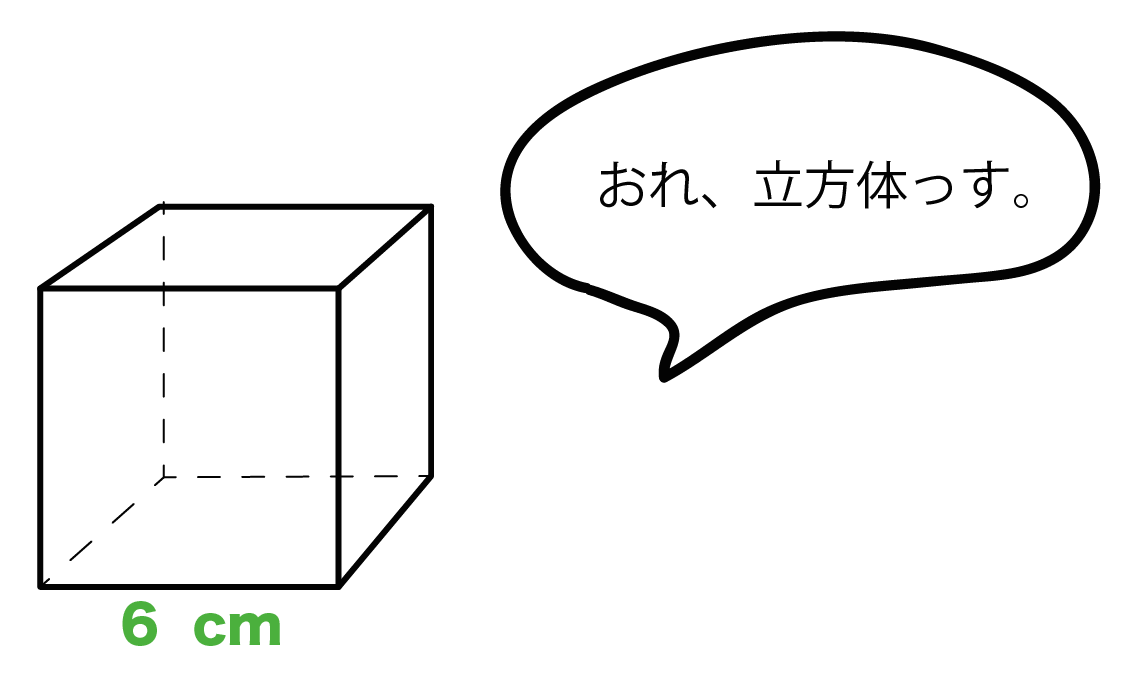



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



無料 中1数学 発展問題 解答プリント 空間図形5 立体の表面積




表面積の求め方 計算公式一覧
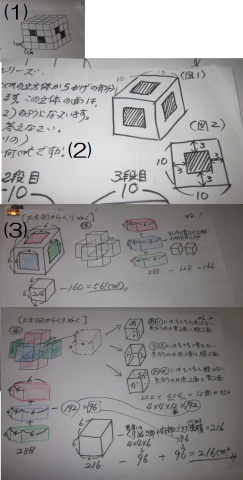



立体のくり抜き 表面積 ようこそ狛江の家庭塾へ




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿